The application of an isotropic crushable foam model to predict the femoral fracture risk

Abstract

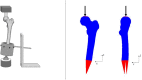
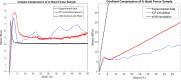
For biomechanical simulations of orthopaedic interventions, it is imperative to implement a material model that can realistically reproduce the nonlinear behavior of the bone structure. However, a proper material model that adequately combines the trabecular and cortical bone response is not yet widely identified. The current paper aims to investigate the possibility of using an isotropic crushable foam (ICF) model dependent on local bone mineral density (BMD) for simulating the femoral fracture risk. The elastoplastic properties of fifty-nine human femoral trabecular cadaveric bone samples were determined and combined with existing cortical bone properties to characterize two forms of the ICF model, a continuous and discontinuous model. Subsequently, the appropriateness of this combined material model was evaluated by simulating femoral fracture experiments, and a comparison with earlier published results of a softening Von-Mises (sVM) material model was made. The obtained mechanical properties of the trabecular bone specimens were comparable to previous findings. Furthermore, the ultimate failure load predicted by the simulations of femoral fractures was on average 79% and 90% for the continuous and discontinuous forms of the ICF model and 82% of the experimental value for the sVM material model. Also, the fracture locations predicted by ICF models were comparable to the experiments. In conclusion, a nonlinear material model dependent on BMD was characterized for human femoral bone. Our findings indicate that the ICF model could predict the femoral bone strength and reproduce the variable fracture locations in the experiments.

Fig 1

The mechanical experiment of the femoral trabecular bone, (a) Harvesting the specimens (b) Positioning of 8 samples in each bone (c) Experimental setup including DIC system (d) Loading configurations, left is the uniaxial and right is confined setup.

Fig 2

The configuration of the femora in experimental set-up [21] (left ) and FEA simulation(right).

Fig 3

The regression analyses of the measured experimental data for femoral trabecular bone: (a) Youngs’s modulus; (b) Yield stress in the uniaxial compression; (c) Yield stress in the confined compression.

Fig 4. Force-displacement data of five cadaveric femora [18].

Fig 5. Continuous and Discontinuous regression of Young’s modulus (left) and Yield stress (right).

Cortical data was adapted from [20].

Fig 6. Stress-strain data of a sample with BMD of 207.5 mg/ml in uniaxial simulation (left) and a BMD of 208.3 mg/ml in confined simulation (right) with two different material models versus experimental results.

Fig 7. The equivalent plastic strain represents permanent deformation of a femoral sample with a BMD of 207.5 mg/ml.

Fig 8. Comparison between the distributions of the equivalent plastic strain, indicating the fracture locations of the FEA models and the actual fracture location in experiment.

The graphs on the right show the force-displacement data of the FEA models and physical experiments. *Images of cadaveric specimens were adapted from [18].