Distributional regression modeling via generalized additive models for location, scale, and shape: An overview through a data set from learning analytics

Abstract

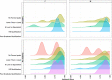
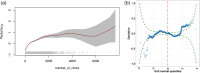
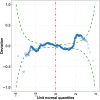
The advent of technological developments is allowing to gather large amounts of data in several research fields. Learning analytics (LA)/educational data mining has access to big observational unstructured data captured from educational settings and relies mostly on unsupervised machine learning (ML) algorithms to make sense of such type of data. Generalized additive models for location, scale, and shape (GAMLSS) are a supervised statistical learning framework that allows modeling all the parameters of the distribution of the response variable with respect to the explanatory variables. This article overviews the power and flexibility of GAMLSS in relation to some ML techniques. Also, GAMLSS' capability to be tailored toward causality via causal regularization is briefly commented. This overview is illustrated via a data set from the field of LA. This article is categorized under:Application Areas > Education and LearningAlgorithmic Development > StatisticsTechnologies > Machine Learning.

Keywords: causal regularization; causality; educational data mining; generalized additive models for location, scale, and shape; learning analytics; machine learning; statistical learning; statistical modeling; supervised learning.

FIGURE 1

Course schedule (timeline occurs in weeks).

FIGURE 2

FAS′ kernel density estimates superimposed on histogram (a) and FAS′ empirical and theoretical CDFs (b). The vertical dotted line in the left plot indicates the variable's mean. The black line in the right plot shows the FAS′ ECDF and the colored lines represent five theoretical CDFs (ranked from best GB1 to worst fit RG). CDF, cumulative distribution functions; ECDF, empirical CDF; GB1, generalized beta type 1; RG, reverse Gumbel.

FIGURE 3

FAS′ kernel density estimates conditioned on the covariates gender (with two levels; F = females and M = males), disability (with two levels; first row = disability, second row = no disability) and highest education (with five levels). The graph also indicates the data are imbalanced in that not all combinations of levels of the covariates have values. That is, while there are FAS values for people with nondisability at all education levels, there are FAS values for people with disabilities at three education levels only.

FIGURE 4

Diagnostic worm plots for assessing the fitness of models using the generalized beta type 1 (GB1) distribution (a), Skew t‐distribution type 2 (ST2) (b), Beta (BE) distribution (c), and Normal (NO) distribution (d) to the FAS variable. A good fit is represented by ≈ 95% of values lying between the two green dotted elliptic lines and close to the deviation value of 0.0. In this example, the GB1 and ST2 distributions fit well most of the data but they struggle to fit the values in the tails of the FAS variable (although the ST2 distribution models better the right tail of the data than the GB1 distribution). However, compared to the GB1 and ST2 models, BE and NO exhibit a poor fit overall.

FIGURE 5

Termplot for the μ submodel when it includes a smooth term (P‐splines) on the covariate “number of clicks” (a). Plot (b) shows the diagnostic worm plot for assessing the fitness of the GB1 model.

FIGURE 6

Worm plot for the GB1 model when the μ, σ, ν, and τ parameters were modeled.

FIGURE 7

Violinplots of the cross‐validation results. The mean and its 95% confidence interval (CI) are represented by the red dots and error bars. The overlaid dot plots, on each violin plot, represent the result of each of the 10‐fold cross‐validation.