This is a preprint.
Beyond Correlation: Optimal Transport Metrics For Characterizing Representational Stability and Remapping in Neurons Encoding Spatial Memory
- PMID: 37503011
- PMCID: PMC10369988
- DOI: 10.1101/2023.07.11.548592
Beyond Correlation: Optimal Transport Metrics For Characterizing Representational Stability and Remapping in Neurons Encoding Spatial Memory
Update in
-
Beyond correlation: optimal transport metrics for characterizing representational stability and remapping in neurons encoding spatial memory.Front Cell Neurosci. 2024 Jan 11;17:1273283. doi: 10.3389/fncel.2023.1273283. eCollection 2023. Front Cell Neurosci. 2024. PMID: 38303974 Free PMC article.
Abstract
Spatial representations in the entorhinal cortex (EC) and hippocampus (HPC) are fundamental to cognitive functions like navigation and memory. These representations, embodied in spatial field maps, dynamically remap in response to environmental changes. However, current methods, such as Pearson's correlation coefficient, struggle to capture the complexity of these remapping events, especially when fields do not overlap, or transformations are non-linear. This limitation hinders our understanding and quantification of remapping, a key aspect of spatial memory function. To address this, we propose a family of metrics based on the Earth Mover's Distance (EMD) as a versatile framework for characterizing remapping. Applied to both normalized and unnormalized distributions, the EMD provides a granular, noise-resistant, and rate-robust description of remapping. This approach enables the identification of specific cell types and the characterization of remapping in various scenarios, including disease models. Furthermore, the EMD's properties can be manipulated to identify spatially tuned cell types and to explore remapping as it relates to alternate information forms such as spatiotemporal coding. By employing approximations of the EMD, we present a feasible, lightweight approach that complements traditional methods. Our findings underscore the potential of the EMD as a powerful tool for enhancing our understanding of remapping in the brain and its implications for spatial navigation, memory studies and beyond.
Keywords: activity maps; grid cell; optimal transport; place cell; remapping; spatial coding; spatiotemporal; stability.
Conflict of interest statement
CONFLICT OF INTEREST STATEMENT The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures





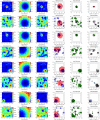

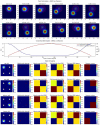

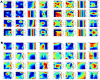
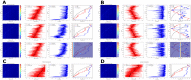
References
-
- Bonneel N., Rabin J., Peyré G., and Pfister H. (2015). Sliced and radon wasserstein barycenters of measures 51, 22–45. doi:10.1007/s10851-014-0506-3 - DOI
-
- Bostock E., Muller R. U., and Kubie J. L. (1991). Experience-dependent modifications of hippocampal place cell firing 1, 193–205. doi:10.1002/hipo.450010207. _eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/hipo.450010207 - DOI - DOI - PubMed
-
- Brandon M. P., Bogaard A. R., Libby C. P., Connerney M. A., Gupta K., and Hasselmo M. E. (2011). Reduction of theta rhythm dissociates grid cell spatial periodicity from directional tuning 332, 595–599. doi:10.1126/science.1201652. Publisher: American Association for the Advancement of Science - DOI - PMC - PubMed
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
