This is a preprint.
A dual Purkinje cell rate and synchrony code sculpts reach kinematics
- PMID: 37503038
- PMCID: PMC10370034
- DOI: 10.1101/2023.07.12.548720
A dual Purkinje cell rate and synchrony code sculpts reach kinematics
Abstract
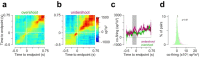
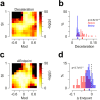
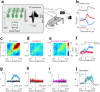
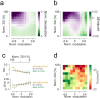
Cerebellar Purkinje cells (PCs) encode movement kinematics in their population firing rates. Firing rate suppression is hypothesized to disinhibit neurons in the cerebellar nuclei, promoting adaptive movement adjustments. Debates persist, however, about whether a second disinhibitory mechanism, PC simple spike synchrony, is a relevant population code. We addressed this question by relating PC rate and synchrony patterns recorded with high density probes, to mouse reach kinematics. We discovered behavioral correlates of PC synchrony that align with a known causal relationship between activity in cerebellar output. Reach deceleration was positively correlated with both Purkinje firing rate decreases and synchrony, consistent with both mechanisms disinhibiting target neurons, which are known to adjust reach velocity. Direct tests of the contribution of each coding scheme to nuclear firing using dynamic clamp, combining physiological rate and synchrony patterns ex vivo, confirmed that physiological levels of PC simple spike synchrony are highly facilitatory for nuclear firing. These findings suggest that PC firing rate and synchrony collaborate to exert fine control of movement.
Conflict of interest statement
Declaration of Interests The authors declare no competing interests.
Figures
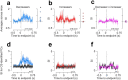
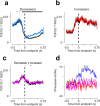
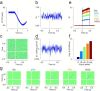
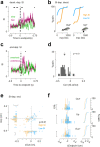



References
-
- Bastian A. J., Martin T. A., Keating J. G. & Thach W. T. Cerebellar ataxia: Abnormal control of interaction torques across multiple joints. J. Neurophysiol. 76, 492–509 (1996). - PubMed
-
- Nashef A., Cohen O., Harel R., Israel Z. & Prut Y. Reversible Block of Cerebellar Outflow Reveals Cortical Circuitry for Motor Coordination. Cell Rep. 27, 2608–2619.e4 (2019). - PubMed
-
- Nashef A., Cohen O., Israel Z., Harel R. & Prut Y. Cerebellar Shaping of Motor Cortical Firing Is Correlated with Timing of Motor Actions. Cell Rep. 23, 1275–1285 (2018). - PubMed
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
