Validation of robust radiobiological optimization algorithms based on the mixed beam model for intensity-modulated carbon-ion therapy
- PMID: 37506069
- PMCID: PMC10381094
- DOI: 10.1371/journal.pone.0288545
Validation of robust radiobiological optimization algorithms based on the mixed beam model for intensity-modulated carbon-ion therapy
Abstract
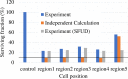
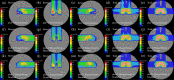
Currently, treatment planning systems (TPSs) that can compute the intensities of intensity-modulated carbon-ion therapy (IMCT) using scanned carbon-ion beams are limited. In the present study, the computational efficacy of the newly designed IMCT algorithms was analyzed for the first time based on the mixed beam model with respect to the physical and biological doses; moreover, the validity and effectiveness of the robust radiobiological optimization were verified. A dose calculation engine was independently generated to validate a clinical dose determined in the TPS. A biological assay was performed using the HSGc-C5 cell line to validate the calculated surviving fraction (SF). Both spot control (SC) and voxel-wise worst-case scenario (WC) algorithms were employed for robust radiobiological optimization followed by their application in a Radiation Therapy Oncology Group benchmark phantom under homogeneous and heterogeneous conditions and a clinical case for range and position errors. Importantly, for the first time, both SC and WC algorithms were implemented in the integrated TPS platform that can compute the intensities of IMCT using scanned carbon-ion beams for robust radiobiological optimization. For assessing the robustness, the difference between the maximum and minimum values of a dose-volume histogram index in the examined error scenarios was considered as a robustness index. The relative biological effectiveness (RBE) determined by the independent dose calculation engine exhibited a -0.6% difference compared with the RBE defined by the TPS at the isocenter, whereas the measured and the calculated SF were similar. Regardless of the objects, compared with the conventional IMCT, the robust radiobiological optimization enhanced the sensitivity of the examined error scenarios by up to 19% for the robustness index. The computational efficacy of the novel IMCT algorithms was verified according to the mixed beam model with respect to the physical and biological doses. The robust radiobiological optimizations lowered the impact of range and position uncertainties considerably in the examined scenarios. The robustness of the WC algorithm was more enhanced compared with that of the SC algorithm. Nevertheless, the SC algorithm can be used as an alternative to the WC IMCT algorithm with respect to the computational cost.
Copyright: © 2023 Yagi et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors, Shinichiro Fujitaka, Shusuke Hirayama, and Hideaki Nihongi are an employee of Hitachi, Ltd.
Figures

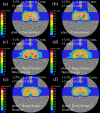
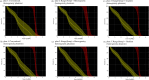
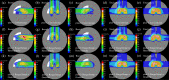
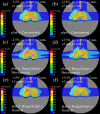
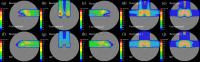
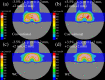
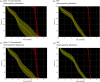

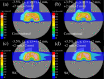

Similar articles
-
Robust optimization for intensity-modulated proton therapy with soft spot sensitivity regularization.Med Phys. 2019 Mar;46(3):1408-1425. doi: 10.1002/mp.13344. Epub 2019 Jan 21. Med Phys. 2019. PMID: 30570164 Free PMC article.
-
Difference in LET-based biological doses between IMPT optimization techniques: Robust and PTV-based optimizations.J Appl Clin Med Phys. 2020 Apr;21(4):42-50. doi: 10.1002/acm2.12844. Epub 2020 Mar 9. J Appl Clin Med Phys. 2020. PMID: 32150329 Free PMC article.
-
Full Monte Carlo-Based Biologic Treatment Plan Optimization System for Intensity Modulated Carbon Ion Therapy on Graphics Processing Unit.Int J Radiat Oncol Biol Phys. 2018 Jan 1;100(1):235-243. doi: 10.1016/j.ijrobp.2017.09.002. Epub 2017 Sep 12. Int J Radiat Oncol Biol Phys. 2018. PMID: 29079118 Free PMC article.
-
Particle arc therapy: Status and potential.Radiother Oncol. 2024 Oct;199:110434. doi: 10.1016/j.radonc.2024.110434. Epub 2024 Jul 14. Radiother Oncol. 2024. PMID: 39009306 Review.
-
Effective radiotherapeutic treatment intensification in patients with pancreatic cancer: higher doses alone, higher RBE or both?Radiat Oncol. 2017 Dec 27;12(1):203. doi: 10.1186/s13014-017-0945-2. Radiat Oncol. 2017. PMID: 29282139 Free PMC article. Review.
Cited by
-
Development and characterization of a dedicated dose monitor for ultrahigh-dose-rate scanned carbon-ion beams.Sci Rep. 2024 May 21;14(1):11574. doi: 10.1038/s41598-024-62148-2. Sci Rep. 2024. PMID: 38773165 Free PMC article.
-
Technical Note: Improving the workflow in a carbon ion therapy center with custom software for enhanced patient care.Tech Innov Patient Support Radiat Oncol. 2024 Apr 23;30:100251. doi: 10.1016/j.tipsro.2024.100251. eCollection 2024 Jun. Tech Innov Patient Support Radiat Oncol. 2024. PMID: 38707713 Free PMC article.
-
Dosimetric impact of stopping power for human bone porosity with dual-energy computed tomography in scanned carbon-ion therapy treatment planning.Sci Rep. 2024 Jul 29;14(1):17440. doi: 10.1038/s41598-024-68312-y. Sci Rep. 2024. PMID: 39075135 Free PMC article.
References
-
- Yagi M, Shimizu S, Minami K, Hamatani N, Tsubouchi T, Takashina M, et al.. Ultra-high Dose-rate Carbon-ion Scanning Beam With a Compact Medical Synchrotron Contributing to Further Development of FLASH Irradiation. Anticancer research. 2023;43(2):581–9. Epub 2023/01/26. doi: 10.21873/anticanres.16194 . - DOI - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Miscellaneous

