Biomechanical Characterisation of Thoracic Ascending Aorta with Preserved Pre-Stresses

Abstract

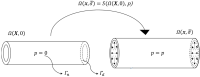
Mechanical properties of an aneurysmatic thoracic aorta are potential markers of future growth and remodelling and can help to estimate the risk of rupture. Aortic geometries obtained from routine medical imaging do not display wall stress distribution and mechanical properties. Mechanical properties for a given vessel may be determined from medical images at different physiological pressures using inverse finite element analysis. However, without considering pre-stresses, the estimation of mechanical properties will lack accuracy. In the present paper, we propose and evaluate a mechanical parameter identification technique, which recovers pre-stresses by determining the zero-pressure configuration of the aortic geometry. We first validated the method on a cylindrical geometry and subsequently applied it to a realistic aortic geometry. The verification of the assessed parameters was performed using synthetically generated reference data for both geometries. The method was able to estimate the true mechanical properties with an accuracy ranging from 98% to 99%.

Keywords: in vivo zero pressure geometry; inverse finite element analysis; pre-stressing algorithm.

Figure 1

Schematic representation of computational domain, $\Omega$, of the cylindrical geometry. The finite element system of equations are solved by a structural solver ($S)$ by applying prescribed displacements at the opening boundaries (${\Gamma }_d)$ and pressure ($p)$ at the inner surface (${\Gamma }_n)$. The general notation for nodes in the undeformed reference configuration and the deformed configuration are represented as $\mathit{X}$ and $\mathit{x}$, respectively, with corresponding stresses as $0$ and $\stackrel{̿}{\sigma }$.

Figure 2

(A) Inner-wall aortic boundaries obtained from 3D DIXON MRI scan and centre-line connecting the lumen at six plane locations. The six plane locations were at root, ascending aorta, before brachiocephalic artery (pre-arch), after left sub-clavian artery (post-arch), descending aorta and at diaphragm levels. (B) Solid mesh ($\Omega ({\mathit{X}}^{\mathit{M}\mathit{R}\mathit{I}},0)$) of the aortic geometry, including the branches. Boundary conditions were applied on the nodes located on ${\Gamma }_{d1}$ to ${\Gamma }_{d4}$ (fixed), ${\Gamma }_{root}$ (fixed/displacement) and ${\Gamma }_n$ (pressure).

Figure 3

Workflow of the algorithm depicting the iterative process of estimating the mechanical parameter $c$ and the scaling factor $\gamma$. The subscript $\mathit{\alpha }$ in ${\mathit{x}}_{\mathit{\alpha },\mathit{d}\mathit{i}\mathit{a}\mathit{s}}^{\mathit{e}\mathit{x}\mathit{p}}$ and ${\mathit{U}}_{\mathit{\alpha }}^{\mathit{d}\mathit{i}\mathit{s}\mathit{p}}$, depict the type of geometry under consideration. In this paper, $\mathit{\alpha }$ = cylinder and aorta.

Figure 4

Steps involved to generate reference data for cylindrical geometry for a given unloaded configuration. (A) Schematic representation of the unloaded configuration $({\mathsf{\Omega }}_0$ = $\Omega ({\mathit{X}}_{\mathit{c}\mathit{y}\mathit{l}\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{r}}^{\mathit{u}\mathit{n}\mathit{l}\mathit{o}\mathit{a}\mathit{d}},0))$, diastolic configuration $({\mathsf{\Omega }}_{dias}=\Omega ({\mathit{x}}_{\mathit{c}\mathit{y}\mathit{l}\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{r},\mathit{d}\mathit{i}\mathit{a}\mathit{s}}^{exp},{\stackrel{=}{\sigma }}_{dias}^{exp}))$ and systolic configuration ${\mathsf{\Omega }}_{sys}=\Omega ({\mathit{x}}_{\mathit{c}\mathit{y}\mathit{l}\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{r},\mathit{s}\mathit{y}\mathit{s}}^{exp},{\stackrel{=}{\sigma }}_{sys}^{exp})$. (B) Finite element simulations depicting the nodes in unloaded (${\mathit{X}}_{\mathit{c}\mathit{y}\mathit{l}\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{r}}^{\mathit{u}\mathit{n}\mathit{l}\mathit{o}\mathit{a}\mathit{d}}$), diastolic (${\mathit{x}}_{\mathit{c}\mathit{y}\mathit{l}\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{r},\mathit{d}\mathit{i}\mathit{a}\mathit{s}}^{\mathit{e}\mathit{x}\mathit{p}}$) and systolic configurations (${\mathit{x}}_{\mathit{c}\mathit{y}\mathit{l}\mathit{i}\mathit{n}\mathit{d}\mathit{e}\mathit{r},\mathit{s}\mathit{y}\mathit{s}}^{\mathit{e}\mathit{x}\mathit{p}}$) associated with ${\mathsf{\Omega }}_0$, ${\mathsf{\Omega }}_{dias}$ and ${\mathsf{\Omega }}_{sys}$.

Figure 5

(A) Four-step procedure to generate reference data for aortic geometry: (i) initial MRI geometry ${\mathsf{\Omega }}_{MRI}$ is inflated (till systolic pressure) to obtain an intermediate geometry ${\mathsf{\Omega }}_{int}$; (ii) unloaded configuration ${\mathsf{\Omega }}_0$ is obtained by subtracting the scaled nodal displacements from MRI geometry ${\mathsf{\Omega }}_{MRI}$; (iii) subsequently pressurising ${\mathsf{\Omega }}_0$ with diastolic and (iv) systolic pressures, resulted in ${\mathsf{\Omega }}_{dias}$ and ${\mathsf{\Omega }}_{sys}$. (B) Finite element simulations depicting the nodes in unloaded (${\mathit{X}}_{\mathit{a}\mathit{o}\mathit{r}\mathit{t}\mathit{a}}^{\mathit{u}\mathit{n}\mathit{l}\mathit{o}\mathit{a}\mathit{d}}$), diastolic (${\mathit{x}}_{\mathit{a}\mathit{o}\mathit{r}\mathit{t}\mathit{a},\mathit{d}\mathit{i}\mathit{a}\mathit{s}}^{\mathit{e}\mathit{x}\mathit{p}}$) and systolic configurations (${\mathit{x}}_{\mathit{a}\mathit{o}\mathit{r}\mathit{t}\mathit{a},\mathit{s}\mathit{y}\mathit{s}}^{\mathit{e}\mathit{x}\mathit{p}}$) associated with ${\mathsf{\Omega }}_0$, ${\mathsf{\Omega }}_{dias}$ and ${\mathsf{\Omega }}_{sys}$.