Young's Experiment with Entangled Bipartite Systems: The Role of Underlying Quantum Velocity Fields

Abstract

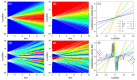
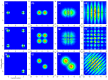
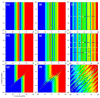
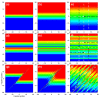
We consider the concept of velocity fields, taken from Bohmian mechanics, to investigate the dynamical effects of entanglement in bipartite realizations of Young's two-slit experiment. In particular, by comparing the behavior exhibited by factorizable two-slit states (cat-type state analogs in the position representation) with the dynamics exhibited by a continuous-variable Bell-type maximally entangled state, we find that, while the velocity fields associated with each particle in the separable scenario are well-defined and act separately on each subspace, in the entangled case there is a strong deformation in the total space that prevents this behavior. Consequently, the trajectories for each subsystem are not constrained any longer to remain confined within the corresponding subspace; rather, they exhibit seemingly wandering behavior across the total space. In this way, within the subspace associated with each particle (that is, when we trace over the other subsystem), not only interference features are washed out, but also the so-called Bohmian non-crossing rule (i.e., particle trajectories are allowed to get across the same point at the same time).

Keywords: Bohmian mechanics; Gaussian wave packet; Young’s interference; bipartite states; cat state; continuous variable entanglement; quantum phase field; transverse velocity field.

Figure 1

Time evolution of a single Gaussian wave packet centered at $x_0=0$ (upper row panels) and a coherent superposition of two Gaussian wave packets with $d=10$ (lower row panels). (a,d) Contour plot of the probability density. In the color code, minimum density (zero) is denoted with blue and maximum with red. For a better visualization, in the case of the superposition state, we consider a truncation to about two thirds of the maximum. (b,e) Contour plot of the transverse velocity field (19). For a better visualization, both the maximum (positive) and minimum (negative) values of the velocity fields were truncated to 1.5 and $-1.5$, respectively. In the color code, these values are denoted with red and blue, respectively, and greenish hues represent zero velocity values and around this. (c,f) Transverse velocity field in terms of the x-coordinate at specific times [see color legend in panel (c); since the yellow line (for $t=1$) overlaps the red one (for $t=0.25$), only the former can be seen in both panels (c) and (f)]. To illustrate the dynamics generated by the velocity field, the Gaussian wave packets in each contour plot are covered by a set of 21 Bohmian trajectories (white solid lines) with equidistant initial conditions. In the two cases, the initial conditions were chosen within the interval $x_c\pm \Delta x$, with $\Delta x=1$, and where $x_c=x_0=0$ for the single Gaussian, and $x_c=x_A,x_B$, with $x_A=-x_B=5$, for the superposition state. The horizontal dashed gray lines in panel (f) indicate the quantized value for the average momentum, $\hslash {\kappa }_n$, determined according to Equation (40), from $n=0,\pm 1,\pm 2$, and $\pm 3$. The numerical values used in the simulations were: ${\sigma }_0=0.5$, $p_0=0$, $m=1$, and $\hslash =1$. See text for further details.

Figure 2

Time evolution of the time-dependent diffusive prefactors of Equations (19) and (23), which rule out, respectively, the slope of the velocity field $v(x,t)$ at a given time (solid black line) and the separation rate $v\left[x\right(t\left)\right]$ of the trajectories with respect to the centroid of the wave packet (solid red line). Although both slopes increase linearly at short times, in the first case a maximum is reached at $t=\tau$ (this characteristic time scale is denoted with the dashed vertical blue line), and then it starts decreasing as $t^{-1}$. In the second case, the slope keeps increases until it reaches an asymptotic constant value, which corresponds to the asymptotic value of the dispersion rate of a Gaussian wave packet, $d{\sigma }_t/dt\approx \hslash /2m{\sigma }_0$ (this is the so-called spreading velocity, as introduced in [31]). The numerical values considered here were: ${\sigma }_0=0.5$, $p_0=0$, $m=1$, and $\hslash =1$.

Figure 3

Contour plots illustrating several stages of the evolution of the probability density for three bipartite systems. Upper row: Uncorrelated bipartite state described by a two-Gaussian superposition for X and single Gaussian for Y. Central row: Uncorrelated bipartite state described by a two-Gaussian superposition for both X and Y. Lower row: Entangled bipartite state described by a Bell-type state. From left to right: $t=0$, $t=2$, $t=4$, and $t=10$. Color code: minimum density (zero) is denoted with blue and maximum with red in all cases. In the first column panels, cross-shaped sets of markers superimposed to each Gaussian distribution denote the ensembles of initial conditions considered in the calculation of Bohmian trajectories. Each horizontal/vertical ensemble contains a total of 21 evenly distributed initial conditions, chosen as follows: for the horizontal ensembles, within the interval $(x_c\pm \Delta x,y_{c^{\prime }})$; for the vertical ensembles, within the interval $(x_c,y_{c^{\prime }}+\Delta y)$. In all cases, $\Delta x=\Delta y=1$, while we have $y_{c^{\prime }}=0$ for the single Gaussians describing Y in the upper panels, and $x_c,y_{c^{\prime }}=x_A,x_B$, with $x_A=-x_B=5$, for the superposition and the entangled states. The markers in the fourth column panels indicate the final position of the corresponding Bohmian trajectories. The numerical values used in the simulations were: $x_0=0$ for the single Gaussian and $d=10$ for the other cases with two Gaussians, ${\sigma }_0=0.5$, $p_0=0$, $m=1$, and $\hslash =1$. See text for further details.

Figure 4

Contour plots illustrating several stages of the evolution of the x-component of the transverse velocity field, $v^X(x,y|t)$, for the three bipartite systems of Figure 3. Upper row: Uncorrelated bipartite state, described by a two-Gaussian superposition for X and a single Gaussian for Y. Central row: Uncorrelated bipartite state, described by a two-Gaussian superposition for both X and Y. Lower row: Entangled bipartite statem described by a Bell-type state. From left to right: $t=2$, $t=4$, and $t=10$. For a better visualization, both the maximum (positive) and minimum (negative) values of the velocity fields represented in the nine snapshots have been truncated to 1.5 and $-1.5$, respectively. In the color code, these values are represented with red and blue, respectively, while greenish hues denote zero (and around) velocity values. The markers in the third column panels indicate the corresponding final position of the sets of Bohmian trajectories referred to in the first column panels of Figure 3. The numerical values used in the simulations were: $x_0=0$ for the single Gaussian and $d=10$ for the other cases with two Gaussians, ${\sigma }_0=0.5$, $p_0=0$, $m=1$, and $\hslash =1$. See text for further details.

Figure 5

Contour plots illustrating several stages of the evolution of the y-component of the transverse velocity field, $v^Y(x,y|t)$, for the three bipartite systems of Figure 3. Upper row: Uncorrelated bipartite state, described by a two-Gaussian superposition for X and single Gaussian for Y. Central row: Uncorrelated bipartite state, described by a two-Gaussian superposition for both X and Y. Lower row: Entangled bipartite state, described by a Bell-type state. From left to right: $t=2$, $t=4$, and $t=10$. For a better visualization, both the maximum (positive) and minimum (negative) values of the velocity fields represented in the nine snapshots were truncated to 1.5 and $-1.5$, respectively. In the color code, these values are represented with red and blue, respectively, while greenish hues denote zero (and around) velocity values. The markers in the third column panels indicate the corresponding final position of the sets of Bohmian trajectories referred to in the first column panels of Figure 3. The numerical values used in the simulations were: $x_0=0$ for the single Gaussian and $d=10$ for other cases with two Gaussians, ${\sigma }_0=0.5$, $p_0=0$, $m=1$, and $\hslash =1$. See text for further details.

Figure 6

Bohmian trajectories illustrating the dynamics associated with the three bipartite systems of Figure 3. Left column: Uncorrelated bipartite state, described by a two-Gaussian superposition for X and single Gaussian for Y. The trajectories for each subsystem are plotted in the top and bottom panels, respectively. Central column: Uncorrelated bipartite state, described by a two-Gaussian superposition for both X and Y. An enlargement of the upper half of the system is shown in the bottom panel. Right column: Entangled bipartite state described by a Bell-type state. An enlargement of the upper half of the system is shown in the bottom panel. As is shown in the corresponding first column panels in Figure 3, the initial conditions were chosen considering 21 equidistant positions either along the x or the y directions, covering the Gaussian wave packets in the manner specified, with more detail, in the caption for that figure. In all plots, the x-component of the trajectories is represented with a solid black line, and the y-component with a solid red line. The numerical values used in the simulations were: $x_0=0$ for the single Gaussian and $d=10$ for other cases with two Gaussians, ${\sigma }_0=0.5$, $p_0=0$, $m=1$, and $\hslash =1$. See text for further details.