Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Jul 21;25(7):1092.
doi: 10.3390/e25071092.

Degree-Based Graph Entropy in Structure-Property Modeling

Sourav Mondal  1   2 , Kinkar Chandra Das  1
Affiliations

Degree-Based Graph Entropy in Structure-Property Modeling

Sourav Mondal et al. Entropy (Basel). .

Abstract

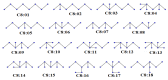
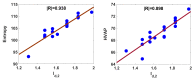
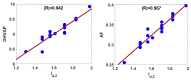
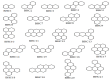
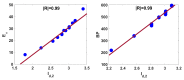
Graph entropy plays an essential role in interpreting the structural information and complexity measure of a network. Let G be a graph of order n. Suppose dG(vi) is degree of the vertex vi for each i=1,2,…,n. Now, the k-th degree-based graph entropy for G is defined as Id,k(G)=-∑i=1ndG(vi)k∑j=1ndG(vj)klogdG(vi)k∑j=1ndG(vj)k, where k is real number. The first-degree-based entropy is generated for k=1, which has been well nurtured in last few years. As ∑j=1ndG(vj)k yields the well-known graph invariant first Zagreb index, the Id,k for k=2 is worthy of investigation. We call this graph entropy as the second-degree-based entropy. The present work aims to investigate the role of Id,2 in structure property modeling of molecules.

Keywords: QSPR analysis; chemical graph theory; entropy; molecular graph; topological index.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Molecular graph representations of octanes.
Figure 2
Figure 2
Linear fitting of Id,2 with entropy and HVAP for octanes.
Figure 3
Figure 3
Linear fitting of Id,2 with DHVAP and AF for octanes.
Figure 4
Figure 4
Experimental vs. predicted AF and residual plot.
Figure 5
Figure 5
Molecular graphs of benzenoid hydrocarbons.
Figure 6
Figure 6
Linear fitting of Id,2 with Eπ and BP for benzenoid hydrocarbons.
Figure 7
Figure 7
Molecular graphs of some chemicals useful in drug preparation.
Figure 8
Figure 8
Linear fitting of Id,2 with BP and MR for some structures displayed in Figure 7.
See this image and copyright information in PMC

References

    1. Gutman I. Degree-based topological indices. Croat. Chem. Acta. 2013;86:351–361. doi: 10.5562/cca2294. - DOI
    1. Shannon C.E., Weaver W. The Mathematical Theory of Communication. University of Illinois Press; Urbana, IL, USA: 1949.
    1. Rashevsky N. Life, information theory, and topology. Bull. Math. Biophys. 1955;17:229–235. doi: 10.1007/BF02477860. - DOI
    1. Dehmer M. Information processing in complex networks: Graph entropy and information functionals. Appl. Math. Comput. 2008;201:82–94. doi: 10.1016/j.amc.2007.12.010. - DOI
    1. Cao S., Dehmer M., Kang Z. Network entropies based on independent sets and matchings. Appl. Math. Comput. 2017;307:265–270. doi: 10.1016/j.amc.2017.02.021. - DOI