Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Jun 30;14(7):1347.
doi: 10.3390/mi14071347.

Numerical Solution of the Electric Field and Dielectrophoresis Force of Electrostatic Traveling Wave System

Yue Yu  1   2 , Yao Luo  3 , Jan Cilliers  1   2 , Kathryn Hadler  1   2 , Stanley Starr  2 , Yanghua Wang  1   2
Affiliations

Numerical Solution of the Electric Field and Dielectrophoresis Force of Electrostatic Traveling Wave System

Yue Yu et al. Micromachines (Basel). .

Abstract

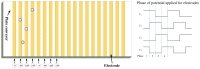
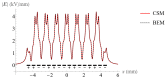
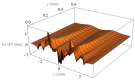
Electrostatic traveling wave (ETW) methods have shown promising performance in dust mitigation of solar panels, particle transport and separation in in situ space resource utilization, cell manipulation, and separation in biology. The ETW field distribution is required to analyze the forces applied to particles and to evaluate ETW design parameters. This study presents the numerical results of the ETW field distribution generated by a parallel electrode array using both the charge simulation method (CSM) and the boundary element method (BEM). A low accumulated error of the CSM is achieved by properly arranging the positions and numbers of contour points and fictitious charges. The BEM can avoid the inconvenience of the charge position required in the CSM. The numerical results show extremely close agreement between the CSM and BEM. For simplification, the method of images is introduced in the implementation of the CSM and BEM. Moreover, analytical formulas are obtained for the integral of Green's function along boundary elements. For further validation, the results are cross-checked using the finite element method (FEM). It is found that discrepancies occur at the ends of the electrode array. Finally, analyses are provided of the electric field and dielectrophoretic (DEP) components. Emphasis is given to the regions close to the electrode surfaces. These results provide guidance for the fabrication of ETW systems for various applications.

Keywords: boundary element method; cell manipulation and separation; charge simulation method; dielectrophoretic force; electric field calculation; electrostatic traveling wave; parallel electrodes.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Diagram showing the typical application system and applied voltage.
Figure 2
Figure 2
Diagram showing the typical application system, consisting of the interdigitated electrode array. D is the electrode width, p is the electrode pitch, and δ is the electrode thickness. The voltage on the boundaries is the example at phase 2.
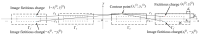
Figure 3
Figure 3
Allocation of contour points and fictitious charges with the method of images.
Figure 4
Figure 4
Electrode geometry for the BEM and the method of images.
Figure 5
Figure 5
Arclength parameters for the element integration.
Figure 6
Figure 6
Comparison of the electric field at the height of 50 μm above the 8 electrodes using the BEM and CSM.
Figure 7
Figure 7
Comparison of the electric field at the height of 50 μm above the 16 electrodes using the BEM and CSM.
Figure 8
Figure 8
Subdivision area illustration.
Figure 9
Figure 9
Comparison of the electric field at the height of 32 μm above the 8 electrodes using the CSM, BEM, and FEM.
Figure 10
Figure 10
Comparison of the electric field at the height of 50 μm above the 16 electrodes using the CSM, BEM, and FEM.
Figure 11
Figure 11
Contour plot of potential and vector plot of electric field above electrodes.
Figure 12
Figure 12
Spatial distribution of the magnitude of field component Ex.
Figure 13
Figure 13
Spatial distribution of the magnitude of field component Ey.
Figure 14
Figure 14
Comparison of the electric field distribution with 18 μm and 180 μm electrode thicknesses (a) at the height of 50 μm above the surface of the conveyor and (b) at the height of 500 μm and 1 mm above the surface of the conveyor.
Figure 15
Figure 15
Contour plot of DEP potential and vector plot of DEP above electrodes in phase 2.
Figure 16
Figure 16
Comparison between DEP and Coulomb force.
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Pohl H.A. The motion and precipitation of suspensoids in divergent electric fields. J. Appl. Phys. 1951;22:869–871. doi: 10.1063/1.1700065. - DOI
    1. Pohl H.A. Some effects of nonuniform fields on dielectrics. J. Appl. Phys. 1958;29:1182–1188. doi: 10.1063/1.1723398. - DOI
    1. Washizu M., Jones T. Multipolar dielectrophoretic force calculation. J. Electrost. 1994;33:187–198. doi: 10.1016/0304-3886(94)90053-1. - DOI
    1. Wang X.-B., Huang Y., Becker F., Gascoyne P. A unified theory of dielectrophoresis and travelling wave dielectrophoresis. J. Phys. D Appl. Phys. 1994;27:1571. doi: 10.1088/0022-3727/27/7/036. - DOI
    1. Taniguchi K., Yamamoto H., Nakano Y., Sakai T., Morikuni S., Watanabe S. A New Technique for Measuring the Distribution of Charge-to-Mass Ration for Toner Particles with On-Line Use. J. Imaging Sci. Technol. 2003;47:224–228. doi: 10.2352/J.ImagingSci.Technol.2003.47.3.art00004. - DOI

LinkOut - more resources