Compressed Gaussian Estimation under Low Precision Numerical Representation

Abstract

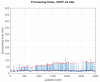
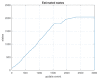
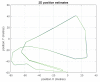
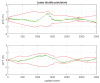
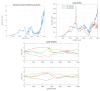
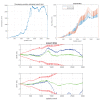
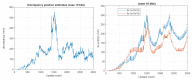
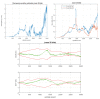
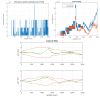
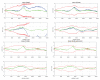
This paper introduces a novel method for computationally efficient Gaussian estimation of high-dimensional problems such as Simultaneous Localization and Mapping (SLAM) processes and for treating certain Stochastic Partial Differential Equations (SPDEs). The authors have presented the Generalized Compressed Kalman Filter (GCKF) framework to reduce the computational complexity of the filters by partitioning the state vector into local and global and compressing the global state updates. The compressed state update, however, still suffers from high computational costs, making it challenging to implement on embedded processors. We propose a low-precision numerical representation for the global filter, such as 16-bit integer or 32-bit single-precision formats for the global covariance matrix, instead of the expensive double-precision, floating-point representation (64 bits). This truncation can inevitably cause filter instability since the truncated covariance matrix becomes overoptimistic or even turns to be an invalid covariance matrix. We introduce a Minimal Covariance Inflation (MCI) method to make the filter consistent while minimizing the truncation errors. Simulation-based experiments results show significant improvement of the proposed method with a reduction in the processing time with minimal loss of accuracy.

Keywords: CEKF; compressed Kalman filter; compressed estimation; high dimensional estimation; integer precision covariance; low precision numerical format.

Figure 1

Best evaluated bounds for $10,000$ cases. For each case, the bound was estimated by binary search. The maximum one was always lower than the proposed $k^{*}=1.25$.

Figure 2

Full view, taken at a certain update event. The blue dots are OOIs (Objects of interest) on the terrain. The traveled path, until that time, is indicated by a red curve.

Figure 3

An image showing, in more detail, the OOI being detected in the previous figure (Broken red segments are used to indicate those visible OOIs.) The scanning sensor has FoV = ${270}^{\circ }$, but occlusions and limited range restrict visibility.

Figure 4

Processing times of the GCKF operating in double precision (in all its components, global low-frequency and high-frequency subsystems) at all update events are shown by the blue line. When a low-frequency global update is required, a peak in the processing time can be seen (indicated by red dots). The average processing time (24 ms), visualised by red dashed line, is well lower than that of a full filter (a standard KF implementation, which is not presented in this work), however, the peaks may represent an issue in many applications (as those peaks reached up to 200 ms with most peaks at 150 ms of processing time).

Figure 5

Processing times of a GCKF operating in low precision (24 bits, having its global PDF component exploiting the single precision bounding approach). The usual peaks, for those updates that require a global update, are well less expensive than those equivalent ones in the full precision standard GCKF. This saving in processing time is achieved at a negligible sacrifice in accuracy. Their implementations of the high-frequency low dimensional individual components are identical. The only difference is related to the low-frequency global component of the GCKF, which maintains the full covariance matrix in a low precision numerical format and bounds it to guarantee estimation consistency.

Figure 6

Number of states in the state vector being estimated, growing during the first phase of the SLAM process, when the map is being explored for its first time. In this part of the test, the SLAM process was in its exploration stage, and new areas were seen for the first time, making the state vector grow in length. The process reached 2 kilo-states.

Figure 7

Platform’s 2D path based on position estimates, for the GCKF SLAM (double and low precision versions). The green trajectory is the actual path.

Figure 8

Discrepancy between ground truth and estimated expected values of the 2D position of the platform, for the standard GCKF process; those are shown in green color. The red curves are the slopes defined by the standard deviations (square roots of the variances of the marginal PDFs). The trip duration is expressed in update events. This figure is relevant for being compared with similar ones achieved by the low precision versions of the GCKF.

Figure 9

Comparing estimates of the standard GCKF and those of the “24 bits GCKF”. The first figure (top-left) shows the discrepancy between expected vehicle positions. The worst case corresponded to a distance of $0.6$ mm. The second (top-right) figure shows the difference in the “marginal standard deviations” (the standard deviations of the estimates of the vehicle positions, as we are not showing here the full joint PDF of the vehicle pose and other states and parameters being estimated by the SLAM process). It can be appreciated that the standard deviations are very similar, those of the low precision GCKF being slightly higher (i.e., more conservative) than those of the standard double precision GCKF. Finally, the last figure (bottom) on the right shows the results of the 24 bits GCKF in the same way previously shown for the standard GCKF in Figure 8. The estimated states of the 24 bits GCKF are almost identical to those of the double precision GCKF.

Figure 10

“8 bits GCKF”. 8 bits, using 7 bits for mantissa and 1 bit for its sign. The maximum discrepancy was large, about $2.5$ meters. The loss of statistical dependency in the global PDF of the GCKF, due to the approximation in the covariance matrix, is too relevant, compromising the convergence of the estimation process. This SLAM process is not able to provide adequate localization accuracy.

Figure 11

“16 bits GCKF”. Similarly, to what is shown in Figure 9, but now for the 16 bits version of the GCKF. The low precision GCKF, i.e., using 16 bits (15 bits mantissa, 1 bit its sign) for representing elements of the global covariance matrix). The maximum discrepancy was about 40 mm. The differences in the generated marginal standard deviations were consistent.

Figure 12

“10 bits GCKF”, whose global component maintains the 10 bits (9 bits mantissa, 1 bit its sign) bounded version of the full global covariance matrix. The maximum discrepancy was about 550 mm.

Figure 12

“10 bits GCKF”, whose global component maintains the 10 bits (9 bits mantissa, 1 bit its sign) bounded version of the full global covariance matrix. The maximum discrepancy was about 550 mm.

Figure 13

“20 bits GCKF”. Case using 20 bits (1 bit for sign, 19 bits for mantissa). Discrepancies are of a few millimeters. However, this numerical format requiring $2.5$ bytes integer is not native but may be of interest for storing results.

Figure 14

“32 bits GCKF”. Case using 32 bits (1 bit for sign, 31 for mantissa). The discrepancy related to position estimates and standard deviations are negligible, with respect to those of the double precision representation (FP64). The maximum discrepancy in the 2D position is lower than $0.008$ mm. This case achieves well superior accuracy to that of the FP32 (which has only 24 bits for mantissa, in contrast to this 32-bit mantissa equivalent, achieved by a 32 bits integer representation used by the 32 “bits GCKF”). This “32 bits” case would correspond to a hypothetical FPXX, located between FP32 and FP64. This 32-bit version is an accurate, in practical terms, replacement for the double precision GCKF.

Figure 15

Shows the standard deviations of the vehicle’s position estimates and the associated error (of the expected values and the ground truth), for the GCKF in 8, 10, 16 bits, and for the double precision one. The sacrifice of precision for the 8 bits version, in the representation of the global covariance matrix, made the estimation process unable to converge. However, with just 16 bits, the estimation process does converge well and is close to the full precision one (not shown here, but it can be appreciated in Figure 11). Bits lengths of 16 or more bits, seemed well appropriate for this estimation problem.