An orthotropic continuum model with substructure evolution for describing bone remodeling: an interpretation of the primary mechanism behind Wolff's law

Abstract

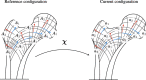
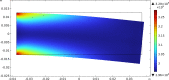
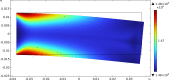
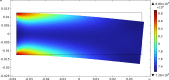
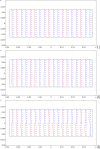
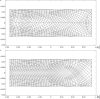
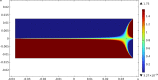
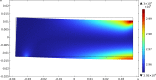
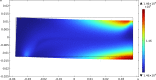
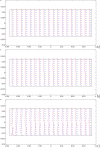
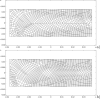
We propose a variational approach that employs a generalized principle of virtual work to estimate both the mechanical response and the changes in living bone tissue during the remodeling process. This approach provides an explanation for the adaptive regulation of the bone substructure in the context of orthotropic material symmetry. We specifically focus upon the crucial gradual adjustment of bone tissue as a structural material that adapts its mechanical features, such as materials stiffnesses and microstructure, in response to the evolving loading conditions. We postulate that the evolution process relies on a feedback mechanism involving multiple stimulus signals. The mechanical and remodeling behavior of bone tissue is clearly a complex process that is difficult to describe within the framework of classical continuum theories. For this reason, a generalized continuum elastic theory is employed as a proper mathematical context for an adequate description of the examined phenomenon. To simplify the investigation, we considered a two-dimensional problem. Numerical simulations have been performed to illustrate bone evolution in a few significant cases: the bending of a rectangular cantilever plate and a three-point flexure test. The results are encouraging because they can replicate the optimization process observed in bone remodeling. The proposed model provides a likely distribution of stiffnesses and accurately represents the arrangement of trabeculae macroscopically described by the orthotropic symmetry directions, as supported by experimental evidence from the trajectorial theory.

Keywords: Bone functional adaptation; Bone remodeling; Growth/resorption processes; Orthotropic constitutive law; Variational formulation.

Fig. 1

Material directions ${\mathit{A}}_i$ in the reference configuration aligned to the trabecula pattern and their images ${\mathit{a}}_i$ under the tensor $\mathit{F}$ for the section of a femur

Fig. 2

Cantilever plate bending test set-up

Fig. 3

Bending test: distribution of ${\beta }_1$ at steady state after the application of the load

Fig. 4

Bending test: distribution of ${\beta }_2$ at steady state after the application of the load

Fig. 5

Bending test: distribution of $\mu$ at steady state after the application of the load

Fig. 6

Bending test: evolution of the material symmetry directions for the bending cantilever test: (1) at the beginning; (2) at an intermediate stage; (3) at the steady-state condition

Fig. 7

Comparison between: a streamlines generated by the unit vectors ${\mathit{A}}_1$ and ${\mathit{A}}_2$; b) isostatic lines for the bending test

Fig. 8

Bending test: difference between the angles between the vectors ${\mathit{A}}_1$ and ${\mathit{A}}_2$ and the eigenvectors of the stress

Fig. 9

Bending test: Enlargement of the vectors ${\mathit{A}}_1$ (blue arrows) and ${\mathit{A}}_2$ (red arrows) in the transition zone

Fig. 10

Three-point flexure test set-up

Fig. 11

Three-point flexure test: distribution of ${\beta }_1$ at steady state after the application of the load

Fig. 12

Three-point flexure test: distribution of ${\beta }_2$ at steady state after the application of the load

Fig. 13

Three-point flexure test: distribution of $\mu$ at steady state after the application of the load

Fig. 14

Three-point flexure test: evolution of the material symmetry directions for the bending cantilever test: a at the beginning; b at an intermediate stage; c at the steady-state condition

Fig. 15

Comparison between: a streamlines generated by the unit vectors ${\mathit{A}}_1$ and ${\mathit{A}}_2$; b isostatic lines for the three-point flexure test

Fig. 16

Three-point flexure test: difference between the angles between the vectors ${\mathit{A}}_1$ and ${\mathit{A}}_2$ and the eigenvectors of the stress