Modeling orientation perception adaptation to altered gravity environments with memory of past sensorimotor states

Abstract

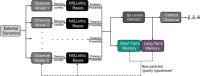
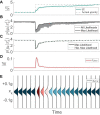
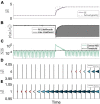
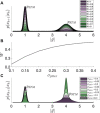
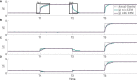
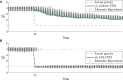
Transitioning between gravitational environments results in a central reinterpretation of sensory information, producing an adapted sensorimotor state suitable for motor actions and perceptions in the new environment. Critically, this central adaptation is not instantaneous, and complete adaptation may require weeks of prolonged exposure to novel environments. To mitigate risks associated with the lagging time course of adaptation (e.g., spatial orientation misperceptions, alterations in locomotor and postural control, and motion sickness), it is critical that we better understand sensorimotor states during adaptation. Recently, efforts have emerged to model human perception of orientation and self-motion during sensorimotor adaptation to new gravity stimuli. While these nascent computational frameworks are well suited for modeling exposure to novel gravitational stimuli, they have yet to distinguish how the central nervous system (CNS) reinterprets sensory information from familiar environmental stimuli (i.e., readaptation). Here, we present a theoretical framework and resulting computational model of vestibular adaptation to gravity transitions which captures the role of implicit memory. This advancement enables faster readaptation to familiar gravitational stimuli, which has been observed in repeat flyers, by considering vestibular signals dependent on the new gravity environment, through Bayesian inference. The evolution and weighting of hypotheses considered by the CNS is modeled via a Rao-Blackwellized particle filter algorithm. Sensorimotor adaptation learning is facilitated by retaining a memory of past harmonious states, represented by a conditional state transition probability density function, which allows the model to consider previously experienced gravity levels (while also dynamically learning new states) when formulating new alternative hypotheses of gravity. In order to demonstrate our theoretical framework and motivate future experiments, we perform a variety of simulations. These simulations demonstrate the effectiveness of this model and its potential to advance our understanding of transitory states during which central reinterpretation occurs, ultimately mitigating the risks associated with the lagging time course of adaptation to gravitational environments.

Keywords: Bayesian; astronaut; internal model (IM); multisensory integration (MSI); otolith; vestibular.

FIGURE 1

Model Framework for adaptation to altered gravity incorporating short term memory (STM) and long-term memory (LTM). The inputs to the model are a time history of body/world dynamics [x, y, and z components of linear acceleration (a) and angular velocity (ω)], and the outputs are the perceived gravity $(\widehat{\mathit{\text{g}}})$, acceleration $(\widehat{\mathit{\text{a}}})$, and angular velocity $(\widehat{\mathrm{\omega }})$. Here and throughout the text, bold denotes a 3D vector.

FIGURE 2

Example evolution of the STM mechanism over time, as proposed by Kravets et al. (2022). (A) The neural estimate of the magnitude of gravity (MAP) initially is identical to the actual magnitude of gravity (1 g). However, when the actual gravity instantly changes to 4 g in this simulation, the internal estimate gradually updates and converges to the proper value. (B) All particle computed likelihoods (gray) as well as the max computed likelihood (black). When the actual magnitude of gravity suddenly changes to 4 g, all of the particles produce low likelihoods. (C) The max likelihood (black) is used to compute a history of max likelihood (HML). (D) The evolution of the standard deviation of the STM function over time. (E) The STM probability density evolving over time. In instances where the history of the max likelihood drops the standard deviation of the probability density function increases. As we have done previously (Kravets et al., 2021), in this figure and throughout, the “Time” on the x-axis does not include units, as it depends on parameters in the model that can be tuned and fit to empirical data in the future.

FIGURE 3

Example evolution of the proposed LTM mechanism over time. (A) The neural estimate of the magnitude of gravity (MAP) is shown, along-side the actual magnitude of gravity. (B) All particle likelihoods (gray) as well as the max likelihood (black). In contrast to the likelihoods at 1 g, the likelihoods following the transition to 4 g span a wider range, as the CNS considers a learned state at 1 g. (C) The central observer’s NIS statistic, which determines whether or not the current estimate is harmonious (i.e., beneath an internal threshold; dashed line). (D) The LTM probability density evolving over time around 4 g. (E) The LTM probability density evolving over time around 1 g. Note that the LTM probability density between 1.05 and 3.95 is negligible (i.e., is 0) and not shown, so between panels (D,E), the entirety of the LTM probability density function is shown. In instances where the current estimate is harmonious, the long-term memory portion of the state transition probability density function (shown here evolving over time) is updated, storing the state information at the current estimate. Probability densities are colored by peak densities to demonstrate emergence and cessation of learned states.

FIGURE 4

(A) Impact of weighting parameter, W, on prioritization of long-term over short-term memory. (B) Modeling W as the solution to a logistic function, dependent on σ_Jitter. (C) The resultant state transition probabilities due to varying levels of jitter, displayed in panel (B).

FIGURE 5

Example simulations showing various adaptation profiles and resulting MAP estimates, both with and without the LTM component of the state transition probability. All simulations begin with an actual gravity level of 1 Earth gravity, and all x-axes are linked to the same timescale. (A) An adaptation to 4 g (see Figure 7), readaptation to 1 g (see Figure 6), and readaptation to 4 g. (B) An adaptation to 4 g after a prolonged stint in 1 g. (C) An adaptation to 2 g, readaptation to 1 g, and an adaptation to 4 g (a second novel hyper-gravity stimulus). (D) An adaptation to 0.5 g, readaptation to 1 g, and an adaptation to 4 g (a second novel gravity stimulus, but where the first was hypo-gravity, and the second is hyper-gravity).

FIGURE 6

Gravity hypothesis generation with and without long-term memory (LTM). The path of gravity adaptation differs between simulations (A) without LTM incorporated and (B) with LTM incorporated, as shown by the small particles/alternate hypotheses at 1 g prior to T2 (see Figure 5A for full gravity transition history). In both panels (A,B), the sizes of the particles are proportional to the posterior probability of each hypothesis at that timestep.

FIGURE 7

Model simulation of tilt perceptions associated with adaptation to gravity transition. (A) highlights the adaptation trajectory surrounding the gravity transition from 1 to 4 g at timepoint T1 in Figure 5, with a roll tilt motion profile. The associated tilt perceptions (or misperceptions) generated by the central observer at time points (B–E) are shown in their respective panels.