Modelling and robust controller design for an underactuated self-balancing robot with uncertain parameter estimation

Abstract

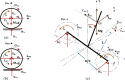
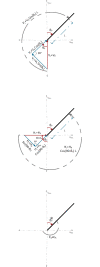
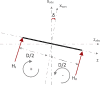
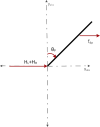
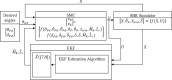
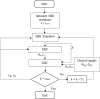
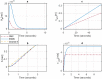
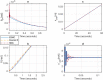
A comprehensive literature review of self-balancing robot (SBR) provides an insight to the strengths and limitations of the available control techniques for different applications. Most of the researchers have not included the payload and its variations in their investigations. To address this problem comprehensively, it was realized that a rigorous mathematical model of the SBR will help to design an effective control for the targeted system. A robust control for a two-wheeled SBR with unknown payload parameters is considered in these investigations. Although, its mechanical design has the advantage of additional maneuverability, however, the robot's stability is affected by changes in the rider's mass and height, which affect the robot's center of gravity (COG). Conventionally, variations in these parameters impact the performance of the controller that are designed with the assumption to operate under nominal values of the rider's mass and height. The proposed solution includes an extended Kalman filter (EKF) based sliding mode controller (SMC) with an extensive mathematical model describing the dynamics of the robot itself and the payload. The rider's mass and height are estimated using EKF and this information is used to improve the control of SBR. Significance of the proposed method is demonstrated by comparing simulation results with the conventional SMC under different scenarios as well as with other techniques in literature. The proposed method shows zero steady state error and no overshoot. Performance of the conventional SMC is improved with controller parameter estimation. Moreover, the stability issue in the reaching phase of the controller is also solved with the availability of parameter estimates. The proposed method is suitable for a wide range of indoor applications with no disturbance. This investigation provides a comprehensive comparison of available techniques to contextualize the proposed method within the scope of self-balancing robots for indoor applications.

Fig 1. Self-balancing robot (SBR) in parking position.

Fig 2

Free body diagram of the self-balancing robot platform (a) left wheel (b) right wheel (c) chassis.

Fig 3

Torque diagram about the z-axis (a) vertical reaction forces between wheels and chassis (b) horizontal reaction forces between wheels and chassis, (c) control torques from left and right wheel.

Fig 4. Torque diagram of the horizontal reaction forces between wheels and chassis about the y-axis.

Fig 5. Force vector diagram of the horizontal reaction forces between wheels & chassis, and the disturbance force at the COG of the robot.

Fig 6. Force vector diagram of the vertical reaction forces between wheels and chassis, F_Cθ, M_g acting at the COG.

Fig 7. Force vector diagram of the components of F_Cθ.

Fig 8. Force vector diagram representing the components of L for the distance traveled along the x-axis.

Fig 9. Force vector diagram representing the components of L for the distance traveled along the y-axis.

Fig 10. Force vector diagram of the chassis representing the yaw angle δ.

Fig 11. Free body diagram of the rider and its contribution to the value of L.

Fig 12. Schematic diagram of a direct current motor.

Fig 13. Flowchart for the extended Kalman filter algorithm.

Fig 14. Block diagram representation of the proposed algorithm for EKF based SMC.

Fig 15. Flow chart for the proposed SBR’s stability control algorithm.

Fig 16

EKF based estimation for the upper limit of (a) rider’s mass, (b) rider’s length.

Fig 17

EKF rider’s estimation for lower limit (a) mass (b) length.

Fig 18

A comparison of system response for case 1: (a) Pitch angle, (b) Yaw angle, (c) Distance, (d) Velocity.

Fig 19

A comparison of system response for case 2: (a) Pitch angle, (b) Yaw angle, (c) Distance, (d) Velocity.

Fig 20

A comparison of system response for case 3: (a) Pitch angle, (b) Yaw angle, (c) Distance, (d) Velocity.

Fig 21

A comparison of system response for case 4: (a) Pitch angle, (b) Yaw angle, (c) Distance, (d) Velocity.

Fig 22. Comparison of the control effort generated by the controllers to stabilize the pitch angle.

Fig 23

A comparison of system response for case 5: (a) Pitch angle, (b) Yaw angle, (c) Distance, (d) Velocity.

Fig 24

A comparison of system response for case 6: (a) Pitch angle, (b) Yaw angle, (c) Distance, (d) Velocity.

Fig 25. Comparison of the control effort generated by the controllers to stabilize the pitch angle.

Fig 26

A comparison of system response for case 7: (a) Pitch angle, (b) Yaw angle, (c) Distance, (d) Velocity.

Fig 27. Comparison of the control effort generated by the controllers to stabilize the pitch angle.

Fig 28. Changes in L and Jr resulting from an incremental 10% increase in Lr and Mr from their nominal values of 1.8 meters and 80 kg, respectively.

Fig 29. The sensitivity of pitch angle resulting from a similar increase in the values of Lr and Mr.