Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Aug 11;13(1):13096.
doi: 10.1038/s41598-023-39756-5.

Magnetohydrodynamic double-diffusive peristaltic flow of radiating fourth-grade nanofluid through a porous medium with viscous dissipation and heat generation/absorption

R A Mohamed  1 , S M Abo-Dahab  1 , A M Abd-Alla  2 , M S Soliman  3
Affiliations

Magnetohydrodynamic double-diffusive peristaltic flow of radiating fourth-grade nanofluid through a porous medium with viscous dissipation and heat generation/absorption

R A Mohamed et al. Sci Rep. .

Abstract

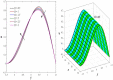
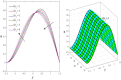
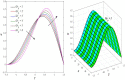
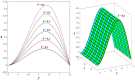
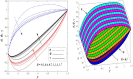
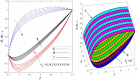
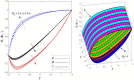
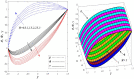
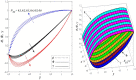
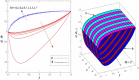
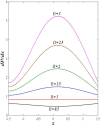
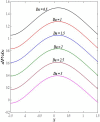
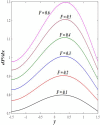
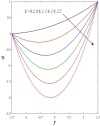
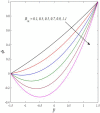
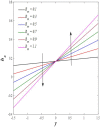
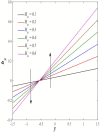
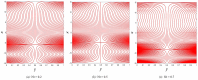
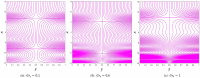
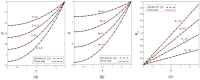
This article focuses on determining how to double diffusion affects the non-Newtonian fourth-grade nanofluids peristaltic motion within a symmetrical vertical elastic channel supported by a suitable porous medium as well as, concentrating on the impact of a few significant actual peculiarities on the development of the peristaltic liquid, such as rotation, initial pressure, non-linear thermal radiation, heat generation/absorption in the presence of viscous dissipation and joule heating with noting that the fluid inside the channel is subject to an externally induced magnetic field, giving it electromagnetic properties. Moreover, the constraints of the long-wavelength approximation and neglecting the wave number along with the low Reynolds number have been used to transform the nonlinear partial differential equations in two dimensions into a system of nonlinear ordinary differential equations in one dimension, which serve as the basic governing equations for fluid motion. The suitable numerical method for solving the new system of ordinary differential equations is the Runge-Kutta fourth-order numerical method with the shooting technique using the code MATLAB program. Using this code, a 2D and 3D graphical analysis was done to show how each physical parameter affected the distributions of axial velocity, temperature, nanoparticle volume fraction, solutal concentration, pressure gradients, induced magnetic field, magnetic forces, and finally the trapping phenomenon. Under the influence of rotation [Formula: see text], heat Grashof number [Formula: see text], solutal Grashof number [Formula: see text], and initial stress [Formula: see text], the axial velocity distribution [Formula: see text] changes from increasing to decreasing, according to some of the study's findings. On the other hand, increasing values of nonlinear thermal radiation [Formula: see text] and temperature ratio [Formula: see text] have a negative impact on the temperature distribution [Formula: see text] but a positive impact on the distributions of nanoparticle volume fraction [Formula: see text] and solutal concentration [Formula: see text]. Darcy number [Formula: see text] and mean fluid rate [Formula: see text] also had a positive effect on the distribution of pressure gradients, making it an increasing function.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interests.

Figures

Figure 1
Figure 1
The geometry of the problem.
Figure 2
Figure 2
Effect of Ω on the axial velocity distribution u (2D and 3D).
Figure 3
Figure 3
Effect of P* on the axial velocity distribution u (2D and 3D).
Figure 4
Figure 4
Effect of Grt on the axial velocity distribution u (2D and 3D).
Figure 5
Figure 5
Effect of Grc on the axial velocity distribution u (2D and 3D).
Figure 6
Figure 6
Effect of Da on the axial velocity distribution u (2D and 3D).
Figure 7
Figure 7
Effect of Grp on the axial velocity distribution u (2D and 3D).
Figure 8
Figure 8
Effect of F on the axial velocity distribution u (2D and 3D).
Figure 9
Figure 9
Effect of R on the distributions of temperature, solutal concentration, and nanoparticles volume fraction (2D and 3D).
Figure 10
Figure 10
Effect of θw on the distributions of temperature, solutal concentration, and nanoparticles volume fraction (2D and 3D).
Figure 11
Figure 11
Effect of Grt on the distributions of temperature, solutal concentration, and nanoparticles volume fraction (2D and 3D).
Figure 12
Figure 12
Effect of Grc on the distributions of temperature, solutal concentration, and nanoparticles volume fraction (2D and 3D).
Figure 13
Figure 13
Effect of Grp on the distributions of temperature, solutal concentration, and nanoparticles volume fraction (2D and 3D).
Figure 14
Figure 14
Effect of Bn on the distributions of temperature, solutal concentration, and nanoparticles volume fraction (2D and 3D).
Figure 15
Figure 15
Effect of Nt on the distributions of temperature, solutal concentration, and nanoparticles volume fraction (2D and 3D).
Figure 16
Figure 16
Effect of M on the distributions of temperature, solutal concentration, and nanoparticles volume fraction (2D and 3D).
Figure 17
Figure 17
Effect of β on the distributions of temperature, solutal concentration, and nanoparticles volume fraction (2D and 3D).
Figure 18
Figure 18
Effect of NFT on the distributions of temperature, solutal concentration, and nanoparticles volume fraction (2D and 3D).
Figure 19
Figure 19
Effect of NTF on the distributions of temperature, solutal concentration, and nanoparticles volume fraction (2D and 3D).
Figure 20
Figure 20
Effect of Nb on the distributions of temperature and nanoparticles volume fraction (2D and 3D).
Figure 21
Figure 21
Pressure gradient distribution for different values of Ω.
Figure 22
Figure 22
Pressure gradient distribution for different values of Da.
Figure 23
Figure 23
Pressure gradient distribution for different values of M.
Figure 24
Figure 24
Pressure gradient distribution for different values of Grt.
Figure 25
Figure 25
Pressure gradient distribution for different values of F.
Figure 26
Figure 26
Magnetic force distribution for different values of E.
Figure 27
Figure 27
Magnetic force distribution for different values of Rm.
Figure 28
Figure 28
Induced magnetic field distribution for different values of E.
Figure 29
Figure 29
Induced magnetic field distribution for different values of Rm.
Figure 30
Figure 30
Induced magnetic field for different values of Ho.
Figure 31
Figure 31
Streamlines profiles for different values of Nb.
Figure 32
Figure 32
Streamlines profiles for different values of Ω.
Figure 33
Figure 33
Streamlines profiles for different values of Da.
Figure 34
Figure 34
Streamlines profiles for different values of Nt.
Figure 35
Figure 35
Streamlines profiles for different values of Grt.
Figure 36
Figure 36
Comparison between Abdalla et al. and the present study.
See this image and copyright information in PMC

References

    1. Latham TW. Fluid Motion in a Peristaltic Pump (Master Thesis) MIT; 1966.
    1. Akram S, Razia A. Hybrid effects of thermal and concentration convection on peristaltic flow of fourth-grade nanofluids in an inclined tapered channel, applications of double-diffusivity. Comput. Model. Eng. Sci. 2021;127:901–919.
    1. Kothandapani M, Pushparaj V, Prakash J. Effect of magnetic field on peristaltic flow of a fourth-grade fluid in a tapered asymmetric channel. J. King Saud Univ. Eng. Sci. 2018;30(1):86–95.
    1. Abdulhadi AM, Ahmed TS. Effect of magnetic field on peristaltic flow of Walters–B fluid through a porous medium in a tapered asymmetric channel. J. Adv. Math. 2017;12:6889–6893.
    1. Asha SK, Deepa CK. Peristaltic flow of a third-grade fluid accounting Joule heating and magnetic field effects in an asymmetric channel. World Sci. News. 2019;137:1–17.