On mathematical modeling of the propagation of a wave ensemble within an individual axon

Abstract

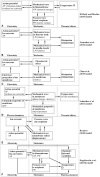
The long history of studying the propagation of an action potential has revealed that an electrical signal is accompanied by mechanical and thermal effects. All these effects together generate an ensemble of waves. The consistent models of such a complex phenomenon can be derived by using properly the fundamental physical principles. In this paper, attention is paid to the analysis of concepts of continuum physics that constitute a basis for deriving the mathematical models which describe the emergence and propagation of a wave ensemble in an axon. Such studies are interdisciplinary and based on biology, physics, mathematics, and chemistry. The governing equations for the action potential together with mechanical and thermal effects are derived starting from basics: Maxwell equations, conservation of momentum, Fourier's law, etc., but modified following experimental studies in electrophysiology. Several ideas from continuum physics like external forces and internal variables can also be used in deriving the corresponding models. Some mathematical concepts used in modeling are also briefly described. A brief overview of several mathematical models is presented that allows us to analyze the present ideas of modeling. Most mathematical models deal with the propagation of signals in a healthy axon. Further analysis is needed for better modeling the pathological situations and the explanation of the influence of the structural details like the myelin sheath or the cytoskeleton in the axoplasm. The future possible trends in improving the models are envisaged.

Keywords: accompanying effects; action potential; interdisciplinary; laws of physics; modeling.

Figure 1

Left panel: Not-to-scale sketch of an axon and the signal ensemble propagation in it. Right panel: A sketch of a nerve cell.

Figure 2

Block schemes for the noted models—(A) El Hady and Machta (2015); (B) Jérusalem et al. (2014); (C) Chen et al. (2019); (D) Schneider (2021); (E) Rvachev (2010); (F) Engelbrecht et al. (2021).