Application of referenced thermodynamic integration to Bayesian model selection

Abstract

Evaluating normalising constants is important across a range of topics in statistical learning, notably Bayesian model selection. However, in many realistic problems this involves the integration of analytically intractable, high-dimensional distributions, and therefore requires the use of stochastic methods such as thermodynamic integration (TI). In this paper we apply a simple but under-appreciated variation of the TI method, here referred to as referenced TI, which computes a single model's normalising constant in an efficient way by using a judiciously chosen reference density. The advantages of the approach and theoretical considerations are set out, along with pedagogical 1 and 2D examples. The approach is shown to be useful in practice when applied to a real problem -to perform model selection for a semi-mechanistic hierarchical Bayesian model of COVID-19 transmission in South Korea involving the integration of a 200D density.

Fig 1. Illustration of steps from the 1D pedagogical example.

A) $q^{\lambda }{q}_{\text{ref}}^{(1-\lambda )}$ for the 1d example density in parameter θ (Eq 9) at selected λ values along the path. B) Expectation ${\mathbb{E}}_{q(\lambda ;\mathit{\theta })}\left[\text{log}\frac{q\left(\mathit{\theta }\right)}{q_{\text{ref}}\left(\mathit{\theta }\right)}\right]$ vs MCMC iteration, shown at each value of λ sampled. C) λ-dependence of ${\mathbb{E}}_{q(\lambda ;\mathit{\theta })}\left[\text{log}\frac{q\left(\mathit{\theta }\right)}{q_{\text{ref}}\left(\mathit{\theta }\right)}\right]$, the TI contribution to the log-evidence. D) Convergence of the evidence z, with 1% convergence after 500 iterations and 0.1% after 17, 000 iterations per λ.

Fig 2. Contour plots of un-normalised densities.

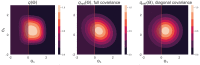
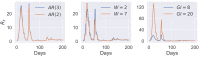
Contour plots of the un-normalised density q and its two reference densities q_ref, one using a full covariance matrix and another using a diagonal covariance matrix that can be easily marginalised. The red line shows the lower boundary θ₁ = 0 and the shaded θ₁ < 0 region to the left of the line is outside of the support of the density q.

Fig 3. The estimated log-evidence of M₂ from the Radiata Pine benchmark problem.

The log-evidence of M₂ from the Radiata Pine benchmark problem is shown estimated using three approaches. (A) shows the rolling mean of log-evidence of M₂ over 1500 iterations per λ obtained by referenced TI (blue line) and PP₁₀₀ (orange line) methods. The exact value is shown with red dashed line. (B) shows the mean log-evidence of the model M₂ evaluated over 15 runs of the three algorithms. The exact value of the log-evidence is shown with the dotted line.

Fig 4. Time-dependent reproduction number.

Time-dependent reproduction number generated by models with the highest evidence calculated using the Laplace approximation (orange lines) and referenced TI (blue lines). Note, the fitting data in this example contains superspreading events (which leads to very high values of R_t on certain days) so is not representative of SARS-CoV-2 transmission generally.