Complex Linear Response Functions for a Multiconfigurational Self-Consistent Field Wave Function in a High Performance Computing Environment

Abstract

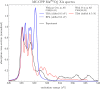
We present novel developments for the highly efficient evaluation of complex linear response functions of a multiconfigurational self-consistent field (MCSCF) wave function as implemented in MultiPsi. Specifically, expressions for the direct evaluation of linear response properties at given frequencies using the complex polarization propagator (CPP) approach have been implemented, within both the Tamm-Dancoff approximation (TDA) and the random phase approximation (RPA). Purely real algebra with symmetric and antisymmetric trial vectors in a shared subspace is used wherein the linear response equations are solved. Two bottlenecks of large scale MC-CPP calculations, namely, the memory footprint and computational time, are addressed. The former is addressed by limiting the size of the subspace of trial vectors by using singular value decomposition (SVD) on either orbital or CI subspaces. The latter is addressed using an efficient parallel implementation as well as the strategy of dynamically adding linear response equations at near-convergence to neighboring roots. Furthermore, a novel methodology for decomposing MC-CPP spectra in terms of intuitive orbital excitations in an approximate fashion is presented. The performance of the code is illustrated with several numerical examples, including the X-ray spectrum of a molecule with nearly one hundred atoms. Additionally, for X-ray spectroscopy, the effect of including or excluding the core orbital in the active space on small covalent metal complexes is discussed.

Figure 1

Porphyrin-A: X = NO, R = SO₃^–; Fe-tetrakis(4-sulfonatophenyl)porphyrin: X = empty, R = SO₃H.

Figure 2

MultiPsi computational time profile showing steps along the algorithm to compute MC-CPP XA spectra of porphyrin-A using a CAS(15,11)/def2-SV(P) wave function. The frequency range is 720 to 730 eV at a resolution of 100 frequencies including all spatial dimensions. Initialization incorporates the SCF, MCSCF steps, and the creation of the initial guess.

Figure 3

Convergence behavior of a single linear response equation of benzene used with a CAS(6,6)/def2-SVPD wave function, at a frequency of 8.35 eV with and without TDA. The inset figure shows CPP spectra at these same levels of theory with the single equation marked in green.

Figure 4

Number of CI and orbital trial vectors in an MC-TDA XA calculation (720 to 730 eV, 100 frequencies, all spatial dimensions) of porphyrin-A with a CAS(15,11)/def2-SV(P) wave function when (a) imposing no limit to subspace size and (b) using the collapse subspace function on the CI or orbital subspaces if either exceeds 400 vectors. The inset in (a) is the calculated XA spectrum.

Figure 5

Solving all MC-CPP equations simultaneously (dashed lines) vs dynamically adding equations near-convergence of neighboring roots (solid lines), tested on benzene using a CAS(6,6)/def2-SVPD wave function. The frequency range is 0 to 18 eV at a resolution of 200 frequencies. Markers indicate at which iteration equations were added.

Figure 6

Scaling performance of the MC-CPP algorithm in MultiPsi tested on Fe-tetrakis(4-sulfonatophenyl)porphyrin using a CAS(7,6)/def2-SV(P) wave function solving for an XA spectrum (between 410 and 417 eV at a resolution of 192 frequencies). Sixteen OpenMP threads (half a node) are used as a starting point, and then the number of MPI ranks is increased to reach 32 full nodes (1024 cores).

Figure 7

MC-CPP XA spectra of Mn^(III)O⁺ between 526 and 540 eV at a resolution of 300 frequencies with and without TDA. Using a wave function without the O 1s in the active space, corresponding to a CAS(10,9) (blue), with the O 1s in the active space, corresponding to a RAS(12,10) (red). A damping constant of 0.16 eV was used, and post-CPP, a Gaussian broadening function with a HWHM of 0.1 eV was applied. The experimental line (black) is taken from ref (38).

Figure 8

MC-CPP XA spectra of Mn^(V)O₂⁺ between 526 and 540 eV at a resolution of 300 frequencies with and without TDA. Using a wave function without the O 1s in the active space, corresponding to a CAS(14,11) (blue), with the O 1s in the active space, corresponding to a RAS(18,13) (red). A damping constant of 0.16 eV was used, and post-CPP, a Gaussian broadening function with a HWHM of 0.1 eV was applied. The experimental line (black) is taken from ref (38).

Figure 9

Excitation character decomposition of Mn^(III)O⁺ RPA (top) and Mn^(V)O₂⁺ TDA XA K-edge spectra (bottom) where (a, c) are without inclusion of the O 1s orbital in the active space and (b, d) are with inclusion of the O 1s orbital in the active space.

Figure 10

MC-TDA CPP simulated XA spectrum of Fe-tetrakis(4-sulfonatophenyl)porphyrin with a CAS(7,6)/def2-SV(P) wave function. The frequency range is 400–420 eV at a resolution of 200 frequencies. A post-CPP Gaussian broadening with an HWHW of 0.9 eV has been applied. The theoretical spectrum has been red-shifted by 18 eV to align with experiment. The experimental line is from ref (40).