Transcriptomic forecasting with neural ordinary differential equations

Abstract

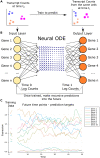
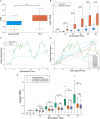
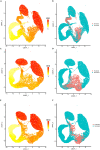
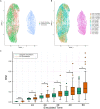
Single-cell transcriptomics technologies can uncover changes in the molecular states that underlie cellular phenotypes. However, understanding the dynamic cellular processes requires extending from inferring trajectories from snapshots of cellular states to estimating temporal changes in cellular gene expression. To address this challenge, we have developed a neural ordinary differential-equation-based method, RNAForecaster, for predicting gene expression states in single cells for multiple future time steps in an embedding-independent manner. We demonstrate that RNAForecaster can accurately predict future expression states in simulated single-cell transcriptomic data with cellular tracking over time. We then show that by using metabolic labeling single-cell RNA sequencing (scRNA-seq) data from constitutively dividing cells, RNAForecaster accurately recapitulates many of the expected changes in gene expression during progression through the cell cycle over a 3-day period. Thus, RNAForecaster enables short-term estimation of future expression states in biological systems from high-throughput datasets with temporal information.

Keywords: artificial intelligence; cellular phenotypes; machine learning; neural ODE; predictive biology; single-cell RNA-seq; temporalomics.

Figure 1

Diagram of RNAForecaster (A) Two count matrices are input to RNAForecaster, each containing the same genes and cells. The counts matrices are from adjacent time points from the same cells, labeled here as t = 0 and t = 1. (B) The t = 0 counts for each cell are input to the input layer of a neural network. The output layer of the neural network has the same number of nodes as the input layer and is compared with the results from the same cell at t = 1. The MSE between the two forms the loss function, which is trained on using an ODE solver to produce a neural ODE. Once the network is trained, the output can be fed into the input layer, allowing for prediction of the expression levels at the next time point, which can be repeated recursively to predict for t time steps. (C) A simulation of the expression levels in a cell, showing 10 genes over 50 time points. RNAForecaster is trained on the first two time points, using multiple cells in order to learn some generalization of the temporal dynamics between genes. RNAForecaster then attempts to estimate expression of each gene at the later time points.

Figure 2

RNAForecaster prediction accuracy in simulated single-cell expression data (A) Comparison of MSE loss on the 20% held-out validation set of predictions from t = 0 to t = 1 between a neural ODE and a five-hidden-layer MLP, over all simulations. (B) Comparison of log MSE loss on the next 50 simulated time points between a neural ODE and a five-hidden-layer MLP. (C) A median example of expression prediction of a single gene in a single cell. The predictions of the neural ODE and MLP are shown. (D) The predictions of 10 different neural ODEs, each trained using a different initialization of stochastic gradient descent, for the same gene and cell as (C). (E) Log MSE loss comparison between a single-network neural ODE vs. the median predictions from a 10- or 25-network ensemble of neural ODEs. ∗∗p < 1e−6 ∗∗∗p < 1e−10. See also Figures S1–S4.

Figure 3

RNAForecaster predicts bifurcation of cells when trained on cells immediately prior to bifurcation (A) UMAP of bifurcating cell simulation across 50 cells from simulated time point 1 to time point 800, plus RNAForecaster’s predictions from time point 366 (just before the bifurcation) through the next 100 time points. Colored by time point. (B) UMAP of same cells as in (A) but colored by whether cells were from the ground-truth simulation or RNAForecaster’s predictions. (C) UMAP of bifurcating cell simulation across 50 cells from simulated time point 1 to time point 800, plus RNAForecaster’s predictions from time point 251 through the next 200 time points. Colored by time point. (D) UMAP of same cells as in (C) but colored by whether cells were from the ground-truth simulation or RNAForecaster’s predictions. (E) UMAP of bifurcating cell simulation across 50 cells from simulated time point 1 to time point 800, plus RNAForecaster’s predictions using the model from (C) and (D), predicted from time point 366 (just before the bifurcation) through the next 100 time points. Colored by time point. (F) UMAP of same cells as in (E), but colored by whether cells were from the ground-truth simulation or RNAForecaster’s predictions.

Figure 4

RNAForecaster can predict the impact of a gene KO that moves cell expression outside the input space (A) A UMAP embedding of the training data from one simulation provided to RNAForecaster alongside the simulated data after a gene KO and RNAForecaster’s estimations of expression states after KO. (B) UMAP from same simulation as (A), labeled by time point and whether a cell was from the pre-KO simulations, post-KO simulation, or post-KO RNAForecaster prediction. (C) Boxplot comparing the MSE loss from the 10 network ensembles shown previously in Figure 2 and the MSE loss from 10 network ensembles onto simulated KO data, where the same gene networks were used to generate the simulations in both cases. ∗p < 0.01 ∗∗p < 1e−6 ∗∗∗p < 1e−10.

Figure 5

Application of RNAForecaster to metabolic labeling single-cell expression data (A) Left is a diagram of the basic concept behind metabolic labeling protocols such as scEU-seq. On the right is a diagram illustrating how the output from metabolic labeling protocols is input to the RNAForecaster neural network. (B) Diagram showing the tricycle cell-cycle scores of each 1-h labeled cell from the Battich et al. scEU-seq retinal epithelium cell cycle dataset. After these cells are used to train RNAForecaster, the future expression states of each cell can be predicted. These expression states can likewise be scored for cell cycle prediction, and we can validate the predictions on whether they generally follow the expected trajectory of the cell cycle.

Figure 6

Performance of RNAForecaster at forecasting the cell cycle (A) Boxplot of a metric describing the order of the tricycle scores of cell cycle state made using RNAForecaster’s predictions of gene expression. A higher score indicates the scores were more aligned with the order of the cell cycle compared with the metric when applied to randomly generated tricycle scores. (B) Barplot of the log-log median total counts per cell in the scEU-seq dataset vs. the output of different neural ODE implementations at the 72-h prediction. (C) Boxplot of the tricycle score order metric for the neural ODE implementations shown in (B). (D–F) Examples of tricycle scores on the RNAForecaster predictions in three cells. ∗p < 0.05 ∗∗p < 0.001 ∗∗∗p < 1e−16. See also Figure S7.