Early adversity changes the economic conditions of mouse structural brain network organization

Abstract

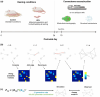
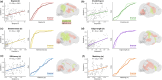
Early adversity can change educational, cognitive, and mental health outcomes. However, the neural processes through which early adversity exerts these effects remain largely unknown. We used generative network modeling of the mouse connectome to test whether unpredictable postnatal stress shifts the constraints that govern the organization of the structural connectome. A model that trades off the wiring cost of long-distance connections with topological homophily (i.e., links between regions with shared neighbors) generated simulations that successfully replicate the rodent connectome. The imposition of early life adversity shifted the best-performing parameter combinations toward zero, heightening the stochastic nature of the generative process. Put simply, unpredictable postnatal stress changes the economic constraints that reproduce rodent connectome organization, introducing greater randomness into the development of the simulations. While this change may constrain the development of cognitive abilities, it could also reflect an adaptive mechanism that facilitates effective responses to future challenges.

Keywords: brain organization; early adversity; generative models; graph theory; structural connectome; unpredictable stress.

FIGURE 1

Experimental design and generative modeling procedure. (a) On postnatal day 0, 49 pups were randomly assigned to a paradigm of unpredictable postnatal stress or standard rearing conditions until postnatal day 26. After postnatal day 70, mice were sacrificed and ex vivo diffusion imaging was performed. Whole‐brain probabilistic tractography was used to reconstruct the structural connectome of each animal. (b) An illustration of the generative process using a simplified connectome of 10 nodes. Starting from a sparse seed network (t = 0), edges are added one at a time until the simulation reaches the number of edges found in the observed connectome (t = e). The matrix of wiring probabilities is updated at each step, allowing for dynamic shifts as the topology of the network emerges. (c) By systematically varying generative rules and parameter combinations, it is possible to identify the topological term K and the parameters η and γ that best simulate the organization of the observed connectome.

FIGURE 2

Relative performance of generative network models in replicating the organization of empirical connectomes. (a) The energy of the top‐performing synthetic networks for each animal (N = 49) across 13 generative rules: a purely spatial model, which considers only the distance between two regions; two homophily models, which also consider a measure of the similarity of the neighborhoods of the respective regions; five clustering‐based models, which compare the clustering coefficients of the regions; and five degree‐based models, which compare their node degree. White points indicate the sample mean. (b) The topological fingerprint (TF) is a correlation matrix of local network statistics, including node degree, clustering coefficient, betweenness centrality, total edge length, local efficiency, and mean matching index. TFs are shown for the empirical networks and the best‐performing rules across the three categories of generative models. Across all four matrices, the value of the correlation can be inferred from the color bar (spans −0.15 [pale lilac] through 0 [white] to 1 [teal]). Correlations shown are the sample average (N = 49). (c) Across the sample (N = 49), homophily achieves lowest ΔTF, a measure of the discrepancy between the correlational structure of the local topology of the simulations and the empirical connectomes, computed using the equation shown.

FIGURE 3

Simulated networks replicate spatial layout of empirical connectomes. Each point in the scatterplots represents the nodal measure for one of the 130 regions of the parcellation, taken as the average value across animals (N = 49). For each of the six measures, a significant positive correlation exists between the nodes of synthetic and empirical networks. A cumulative density function of the measure is also displayed, as well as a visualization of the mouse brain in which the five regions with the lowest and highest error (i.e., discrepancy between synthetic and empirical networks) are highlighted in green and red, respectively. Four of the statistics ([a] node degree, [b] clustering coefficient, [c] betweenness centrality, and [d] total edge length) are terms of the energy equation used to assess the fit of the synthetic networks, while the remaining statistics ([e] local efficiency and [f] mean matching index) are not.

FIGURE 4

Adversity attenuates optimal generative modeling parameters. (a) In the first run of the homophily model, 160,000 unique combinations of cost parameter η and value parameter γ were tested. The energy surface shown is the sample average (N = 49). (b) Optimal values of η and γ produce the lowest energy synthetic networks. Values were obtained by testing an additional 40,000 parameter combinations in a narrow low‐energy window of the initial grid search, highlighted with a black rectangle in panel (a). Each data point in the scatterplot represents a single animal. Density plots above and to the right highlight differences between unpredictable postnatal stress (UPS) and control conditions. Optimal parameters tend to fall closer to the origin—at the bottom right of the plot—for animals in the UPS condition (ANOVA F _1, 47 = 5.700, p = .021).

FIGURE 5

Weaker wiring constraints heighten stochasticity of network development. (a) Distributions of wiring probabilities ($P_{i,j}$) within the probability matrix, taken as the group averages across all steps of optimal simulations. The unpredictable postnatal stress (UPS) condition shows a flatter distribution with greater dispersion, corresponding to more connections with higher wiring probabilities. (b) Variance among values in the probability matrix ($P_{i,j}$) corresponds to the dispersion of likelihoods of potential future connections. Wiring probability variance rises as simulations develop, especially in the UPS condition, indicating that model stochasticity was more pronounced later in the process. (c) To assess the effect of systematically manipulating wiring constraints, simulations were run at 10% increments from the optimal values for each animal to zero. This resulted in the 490 parameter combinations plotted in this space. (d) Distributions of wiring probabilities ($P_{i,j}$) within the probability matrix, taken as the average across all steps, at each parameter interval. Wiring probabilities for simulations with weaker parameters approach a normal distribution. (e) Topological dissimilarity (ΔTF; see Section 2) was averaged across 1000 randomly wired networks. The organization of simulated networks gradually resembles random topology as parameters approach zero. The same trend is observed when comparing the UPS condition to the control condition, both for (f) optimal generative models and (g) biological connectomes derived through tractography.