Geometric framework to predict structure from function in neural networks
- PMID: 37635906
- PMCID: PMC10456994
- DOI: 10.1103/physrevresearch.4.023255
Geometric framework to predict structure from function in neural networks
Abstract
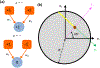
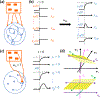
Neural computation in biological and artificial networks relies on the nonlinear summation of many inputs. The structural connectivity matrix of synaptic weights between neurons is a critical determinant of overall network function, but quantitative links between neural network structure and function are complex and subtle. For example, many networks can give rise to similar functional responses, and the same network can function differently depending on context. Whether certain patterns of synaptic connectivity are required to generate specific network-level computations is largely unknown. Here we introduce a geometric framework for identifying synaptic connections required by steady-state responses in recurrent networks of threshold-linear neurons. Assuming that the number of specified response patterns does not exceed the number of input synapses, we analytically calculate the solution space of all feedforward and recurrent connectivity matrices that can generate the specified responses from the network inputs. A generalization accounting for noise further reveals that the solution space geometry can undergo topological transitions as the allowed error increases, which could provide insight into both neuroscience and machine learning. We ultimately use this geometric characterization to derive certainty conditions guaranteeing a nonzero synapse between neurons. Our theoretical framework could thus be applied to neural activity data to make rigorous anatomical predictions that follow generally from the model architecture.
Figures

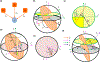

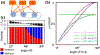



Similar articles
-
Neural learning rules for generating flexible predictions and computing the successor representation.Elife. 2023 Mar 16;12:e80680. doi: 10.7554/eLife.80680. Elife. 2023. PMID: 36928104 Free PMC article.
-
Neural Classifiers with Limited Connectivity and Recurrent Readouts.J Neurosci. 2018 Nov 14;38(46):9900-9924. doi: 10.1523/JNEUROSCI.3506-17.2018. Epub 2018 Sep 24. J Neurosci. 2018. PMID: 30249794 Free PMC article.
-
Excitable networks for finite state computation with continuous time recurrent neural networks.Biol Cybern. 2021 Oct;115(5):519-538. doi: 10.1007/s00422-021-00895-5. Epub 2021 Oct 5. Biol Cybern. 2021. PMID: 34608540 Free PMC article.
-
Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research.J Pharm Biomed Anal. 2000 Jun;22(5):717-27. doi: 10.1016/s0731-7085(99)00272-1. J Pharm Biomed Anal. 2000. PMID: 10815714 Review.
-
Simple Recurrent Networks are Interactive.Psychon Bull Rev. 2025 Jun;32(3):1032-1040. doi: 10.3758/s13423-024-02608-y. Epub 2024 Nov 13. Psychon Bull Rev. 2025. PMID: 39537950 Review.
Cited by
-
Maintaining and updating accurate internal representations of continuous variables with a handful of neurons.Nat Neurosci. 2024 Nov;27(11):2207-2217. doi: 10.1038/s41593-024-01766-5. Epub 2024 Oct 3. Nat Neurosci. 2024. PMID: 39363052 Free PMC article.
-
Vertebrate behavioral thermoregulation: knowledge and future directions.Neurophotonics. 2024 Jul;11(3):033409. doi: 10.1117/1.NPh.11.3.033409. Epub 2024 May 20. Neurophotonics. 2024. PMID: 38769950 Free PMC article. Review.
-
A vast space of compact strategies for effective decisions.Sci Adv. 2024 Jun 21;10(25):eadj4064. doi: 10.1126/sciadv.adj4064. Epub 2024 Jun 21. Sci Adv. 2024. PMID: 38905348 Free PMC article.
-
The mechanics of correlated variability in segregated cortical excitatory subnetworks.bioRxiv [Preprint]. 2023 Apr 27:2023.04.25.538323. doi: 10.1101/2023.04.25.538323. bioRxiv. 2023. Update in: Proc Natl Acad Sci U S A. 2024 Jul 9;121(28):e2306800121. doi: 10.1073/pnas.2306800121. PMID: 37162867 Free PMC article. Updated. Preprint.
-
Graph rules for recurrent neural network dynamics: extended version.ArXiv [Preprint]. 2023 Jan 30:arXiv:2301.12638v1. ArXiv. 2023. PMID: 36776822 Free PMC article. Preprint. No abstract available.
References
-
- Watson JD and Crick FHC, Molecular structure of nucleic acids, Nature (London) 171, 737 (1953). - PubMed
-
- Milo R et al., Network motifs: Simple building blocks of complex networks, Science 298, 824 (2002). - PubMed
-
- Hunter P and Nielsen P, A strategy for integrative computational physiology, Physiology 20, 316 (2005). - PubMed
-
- Seung HS, Reading the book of memory: Sparse sampling versus dense mapping of connectomes, Neuron 62, 17 (2009). - PubMed
-
- Bargmann CI and Marder E, From the connectome to brain function, Nat. Methods 10, 483 (2013). - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
