Topological Superconductors from a Materials Perspective
- PMID: 37637011
- PMCID: PMC10448998
- DOI: 10.1021/acs.chemmater.3c00713
Topological Superconductors from a Materials Perspective
Abstract
Topological superconductors (TSCs) have garnered significant research and industry attention in the past two decades. By hosting Majorana bound states which can be used as qubits that are robust against local perturbations, TSCs offer a promising platform toward (nonuniversal) topological quantum computation. However, there has been a scarcity of TSC candidates, and the experimental signatures that identify a TSC are often elusive. In this Perspective, after a short review of the TSC basics and theories, we provide an overview of the TSC materials candidates, including natural compounds and synthetic material systems. We further introduce various experimental techniques to probe TSCs, focusing on how a system is identified as a TSC candidate and why a conclusive answer is often challenging to draw. We conclude by calling for new experimental signatures and stronger computational support to accelerate the search for new TSC candidates.
© 2023 The Authors. Published by American Chemical Society.
Conflict of interest statement
The authors declare no competing financial interest.
Figures


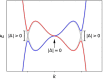
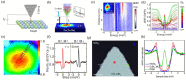

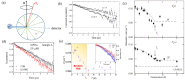
References
-
- Hasan M. Z.; Kane C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. 10.1103/RevModPhys.82.3045. - DOI
-
- Qi X.-L.; Zhang S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. 10.1103/RevModPhys.83.1057. - DOI
-
- Manna K.; Sun Y.; Muechler L.; Kubler J.; Felser C. Heusler, Weyl and Berry. Nat. Rev. Mater. 2018, 3 (8), 244–256. 10.1038/s41578-018-0036-5. - DOI
-
- Armitage N. P.; Mele E. J.; Vishwanath A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90, 015001.10.1103/RevModPhys.90.015001. - DOI
Publication types
LinkOut - more resources
Full Text Sources
Miscellaneous
