Neural network models for influenza forecasting with associated uncertainty using Web search activity trends
- PMID: 37639427
- PMCID: PMC10491400
- DOI: 10.1371/journal.pcbi.1011392
Neural network models for influenza forecasting with associated uncertainty using Web search activity trends
Abstract
Influenza affects millions of people every year. It causes a considerable amount of medical visits and hospitalisations as well as hundreds of thousands of deaths. Forecasting influenza prevalence with good accuracy can significantly help public health agencies to timely react to seasonal or novel strain epidemics. Although significant progress has been made, influenza forecasting remains a challenging modelling task. In this paper, we propose a methodological framework that improves over the state-of-the-art forecasting accuracy of influenza-like illness (ILI) rates in the United States. We achieve this by using Web search activity time series in conjunction with historical ILI rates as observations for training neural network (NN) architectures. The proposed models incorporate Bayesian layers to produce associated uncertainty intervals to their forecast estimates, positioning themselves as legitimate complementary solutions to more conventional approaches. The best performing NN, referred to as the iterative recurrent neural network (IRNN) architecture, reduces mean absolute error by 10.3% and improves skill by 17.1% on average in nowcasting and forecasting tasks across 4 consecutive flu seasons.
Copyright: © 2023 Morris et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures

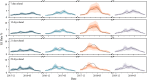
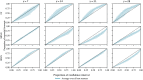
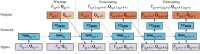
References
-
- Ferguson NM, Laydon D, Nedjati-Gilani G, Imai N, Ainslie K, Baguelin M, et al.. Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. Imperial College COVID-19 Response Team London. 2020;.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

