Paleomass for R-bracketing body volume of marine vertebrates with 3D models

Abstract

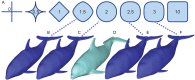
Body mass is arguably the most important characteristic of an organism, yet it is often not available in biological samples that have been skeletonized, liquid-preserved, or fossilized. The lack of information is especially problematic for fossil species, for which individuals with body mass information are not available anywhere. Multiple methods are available for estimating the body mass of fossil terrestrial vertebrates but those for their marine counterparts are limited. Paleomass is a software tool for estimating the body mass of marine vertebrates from their orthogonal silhouettes through bracketing. It generates a set of two 3D models from these silhouettes, assuming superelliptical body cross-sections with different exponent values. By setting the exponents appropriately, it is possible to bracket the true volume of the animal between those of the two models. The original version phased out together with the language platform it used. A new version is reported here as an open-source package based on the R scripting language. It inherits the underlying principles of the original version but has been completely rewritten with a new architecture. For example, it first produces 3D mesh models of the animal and then measures their volumes and areas with the VCG library, unlike the original version that did not produce a 3D model but instead computed the volume and area segment by segment using parametric equations. The new version also exports 3D models in polygon meshes, allowing later tests by other software. Other improvements include the use of NACA foil sections for hydrofoils such as flippers, and optional interpolation with local regression. The software has a high accuracy, with the mean absolute errors of 1.33% when the silhouettes of the animals are known.

Keywords: Body mass estimation; Body silhouette; Marine vertebrate; R; Software; Superellipse.

Figure 1. How superellipses of different exponent values are used to bracket the true volume of a marine vertebrate.

(A) Variations of superelliptical shapes, with numbers being the exponents used to produce respective shapes. (B) A skinny dolphin model with an n value of 1.5 based on the silhouettes from D. (C) Same with an exponent of 2.0. (D) 3D model of Tursiops truncatus (model 61 from digitallife3d.org). (E) A fat model with an exponent of2.5. (F) Same with an exponent of 3.0.

Figure 2. Shape input images from Sphyrna lewini.

(A) Orthogonal views of the target animal, with the overall outlines traced in red. (B) Planar views of fins that are angled in A, with fins in question outlined in red. (C) Input images for Paleomass based on A and B, where fins are separated from the main body. Scale bar in 10 cm. A resulting Paleomass mode is found in Fig. 3E. Image source: A and B are orthographic projections of a 3D model from FFish.asia (Kano et al., 2013; https://sketchfab.com/3d-models/scalloped-hammerhead-shark-s-lewini-5de0eec2e8e0462f9a856124761e0ed8; CC BY 4.0, https://creativecommons.org/licenses/by/4.0/).

Figure 3. Range of body morphologies modelled by Paleomass.

(A) Tursiops truncatus. (B) Stenopterygius quadriscissus. (C) Chaohusaurus chaoxianensis. (D) Rhincodon typus. (E) Sphyrna lewini. (F) Plesiopterys guilelmiimperatoris. (G) Anguilla marmorata. (H) Eopsetta grigorjewi. (I) Latolabrax japonicus. (J) Caranx sexfasciatus.

Figure 4. Computation process of main body and fin/flipper 3D meshes with examples from Cephalorhynchus heavisidii.

(A) Lateral silhouette image input. (B) Dorso-ventral silhouette image input. (C) Coordinates around A in dots, with dorso-ventral diameters in lines, down-sampled to one in every ten coordinates for visualization purposes. (D) Same as C but based on B. (E) Serial superelliptical sections based on diameters from C and D, with an exponent of 2, downsampled at the same rate as in C. (F) Same as E but with an exponent of 3. (G) 3D mesh combining all superelliptical slices as in E but without downsampling. (H) Same as G but based on F. (I) Same as G but with interpolation with local regression with a nearest neighbor parameter of 0.1. (J) Same as H but with interpolation with local regression. (K) Planar silhouette image input. (L) Coordinates around A in dots, with chords in lines. Downsampled to one in every five slices for visualization purposes. (M) Serial foil section based on NACA 0020, downsampled at the same rate as in L. (N) 3D mesh that connected serial foil sections as in C but without downsampling. (O) Same as C but with interpolation with a nearest neighbor parameter of 0.05. (M)–(O) are slightly tilted for visualization purposes and thus appear narrower anteroposteriorly than K–L.

Figure 5. Errors from volume and surface area estimates for a sphere and prolate spheroid depending on the input image resolution.

(A) Errors from the sphere. (B) Errors from a prolate spheroid whose major axis is five times the minor axis. Blue lines are for the surface area and black for the volume. The independent is the number of pixels along the long axis of the geometry, i.e., pixels per diameter.

Figure 6. Optimal superelliptical exponents for 25 species of extant marine vertebrates, with coronal views of five species.

Horizontal bars indicate the range of optimal superelliptical exponents for individual species. Coronal views are given for the following species. (A) Mustelus manazo. (B) Phocoena phocoena. (C) Clupea pallasii. (D) Auxis thazad. (E) Salvelinus leucomaenis. Species with V-shaped ventral halves of the coronal views, e.g., C, tend to have lower exponent values than those with U-shaped ventral halves, such as E. Squares associated with coronal views are each 1 cm.