Phenotype Control techniques for Boolean gene regulatory networks
- PMID: 37646851
- PMCID: PMC10542862
- DOI: 10.1007/s11538-023-01197-6
Phenotype Control techniques for Boolean gene regulatory networks
Abstract
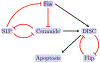
Modeling cell signal transduction pathways via Boolean networks (BNs) has become an established method for analyzing intracellular communications over the last few decades. What's more, BNs provide a course-grained approach, not only to understanding molecular communications, but also for targeting pathway components that alter the long-term outcomes of the system. This has come to be known as phenotype control theory. In this review we study the interplay of various approaches for controlling gene regulatory networks such as: algebraic methods, control kernel, feedback vertex set, and stable motifs. The study will also include comparative discussion between the methods, using an established cancer model of T-Cell Large Granular Lymphocyte Leukemia. Further, we explore possible options for making the control search more efficient using reduction and modularity. Finally, we will include challenges presented such as the complexity and the availability of software for implementing each of these control techniques.
Keywords: Boolean networks; Discrete dynamical systems; Network dynamics; Phenotype control theory; Regulatory networks.
© 2023. The Author(s), under exclusive licence to Society for Mathematical Biology.
Figures



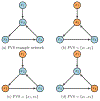
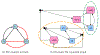
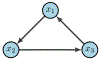
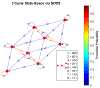


Update of
-
Phenotype control techniques for Boolean gene regulatory networks.bioRxiv [Preprint]. 2023 Apr 18:2023.04.17.537158. doi: 10.1101/2023.04.17.537158. bioRxiv. 2023. Update in: Bull Math Biol. 2023 Aug 30;85(10):89. doi: 10.1007/s11538-023-01197-6. PMID: 37131770 Free PMC article. Updated. Preprint.
Similar articles
-
Phenotype control techniques for Boolean gene regulatory networks.bioRxiv [Preprint]. 2023 Apr 18:2023.04.17.537158. doi: 10.1101/2023.04.17.537158. bioRxiv. 2023. Update in: Bull Math Biol. 2023 Aug 30;85(10):89. doi: 10.1007/s11538-023-01197-6. PMID: 37131770 Free PMC article. Updated. Preprint.
-
Control of Intracellular Molecular Networks Using Algebraic Methods.Bull Math Biol. 2019 Dec 23;82(1):2. doi: 10.1007/s11538-019-00679-w. Bull Math Biol. 2019. PMID: 31919596 Free PMC article.
-
Algebraic model checking for Boolean gene regulatory networks.Adv Exp Med Biol. 2011;696:113-22. doi: 10.1007/978-1-4419-7046-6_12. Adv Exp Med Biol. 2011. PMID: 21431552
-
Boolean network models of cellular regulation: prospects and limitations.J R Soc Interface. 2008 Aug 6;5 Suppl 1(Suppl 1):S85-94. doi: 10.1098/rsif.2008.0132.focus. J R Soc Interface. 2008. PMID: 18508746 Free PMC article. Review.
-
Multi-parameter exploration of dynamics of regulatory networks.Biosystems. 2020 Apr;190:104113. doi: 10.1016/j.biosystems.2020.104113. Epub 2020 Feb 10. Biosystems. 2020. PMID: 32057819 Free PMC article. Review.
Cited by
-
Pancreatic cancer mutationscape: revealing the link between modular restructuring and intervention efficacy amidst common mutations.bioRxiv [Preprint]. 2024 May 22:2024.01.27.577546. doi: 10.1101/2024.01.27.577546. bioRxiv. 2024. Update in: NPJ Syst Biol Appl. 2024 Jul 13;10(1):74. doi: 10.1038/s41540-024-00398-6. PMID: 38352601 Free PMC article. Updated. Preprint.
-
Modular control of Boolean network models.ArXiv [Preprint]. 2024 Nov 4:arXiv:2401.12477v3. ArXiv. 2024. Update in: Bull Math Biol. 2025 Jun 3;87(7):91. doi: 10.1007/s11538-025-01471-9. PMID: 38344220 Free PMC article. Updated. Preprint.
-
Single-cell profiling of EZH2-mediated immune signaling perturbations in NSCLC.bioRxiv [Preprint]. 2025 Jul 17:2025.07.12.663845. doi: 10.1101/2025.07.12.663845. bioRxiv. 2025. PMID: 40791397 Free PMC article. Preprint.
-
Modular Control of Boolean Network Models.Bull Math Biol. 2025 Jun 3;87(7):91. doi: 10.1007/s11538-025-01471-9. Bull Math Biol. 2025. PMID: 40461704 Free PMC article.
-
Cancer mutationscape: revealing the link between modular restructuring and intervention efficacy among mutations.NPJ Syst Biol Appl. 2024 Jul 13;10(1):74. doi: 10.1038/s41540-024-00398-6. NPJ Syst Biol Appl. 2024. PMID: 39003264 Free PMC article.
References
-
- Akutsu T, Hayashida M, Ching W-K, Michael KN (2007) Control of Boolean networks: hardness results and algorithms for tree structured networks. J Theor Biol 244(4):670–679 - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

