Steady-state approximations for Hodgkin-Huxley cell models: Reduction of order for uterine smooth muscle cell model
- PMID: 37647265
- PMCID: PMC10468033
- DOI: 10.1371/journal.pcbi.1011359
Steady-state approximations for Hodgkin-Huxley cell models: Reduction of order for uterine smooth muscle cell model
Abstract
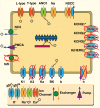
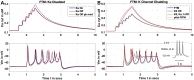
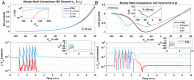
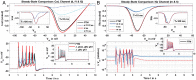
Multi-scale mathematical bioelectrical models of organs such as the uterus, stomach or heart present challenges both for accuracy and computational tractability. These multi-scale models are typically founded on models of biological cells derived from the classic Hodkgin-Huxley (HH) formalism. Ion channel behaviour is tracked with dynamical variables representing activation or inactivation of currents that relax to steady-state dependencies on cellular membrane voltage. Timescales for relaxation may be orders of magnitude faster than companion ion channel variables or phenomena of physiological interest for the entire cell (such as bursting sequences of action potentials) or the entire organ (such as electromechanical coordination). Exploiting these time scales with steady-state approximations for relatively fast-acting systems is a well-known but often overlooked approach as evidenced by recent published models. We thus investigate feasibility of an extensive reduction of order for an HH-type cell model with steady-state approximations to the full dynamical activation and inactivation ion channel variables. Our effort utilises a published comprehensive uterine smooth muscle cell model that encompasses 19 ordinary differential equations and 105 formulations overall. The numerous ion channel submodels in the published model exhibit relaxation times ranging from order 10-1 to 105 milliseconds. Substitution of the faster dynamic variables with steady-state formulations demonstrates both an accurate reproduction of the full model and substantial improvements in time-to-solve, for test cases performed. Our demonstration here of an effective and relatively straightforward reduction method underlines the particular importance of considering time scales for model simplification before embarking on large-scale computations or parameter sweeps. As a preliminary complement to more intensive reduction of order methods such as parameter sensitivity and bifurcation analysis, this approach can rapidly and accurately improve computational tractability for challenging multi-scale organ modelling efforts.
Copyright: © 2023 Means et al. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Conflict of interest statement
The authors have declared that no competing interests exist.
Figures


Similar articles
-
Molecular aspects of electrical excitation in lipid bilayers and cell membranes.Horiz Biochem Biophys. 1976;2:230-84. Horiz Biochem Biophys. 1976. PMID: 776770 Review.
-
Stochastic differential equation model for cerebellar granule cell excitability.PLoS Comput Biol. 2008 Feb 29;4(2):e1000004. doi: 10.1371/journal.pcbi.1000004. PLoS Comput Biol. 2008. PMID: 18463700 Free PMC article.
-
Altered neuronal excitability in a Hodgkin-Huxley model incorporating channelopathies of the delayed rectifier potassium channel.J Comput Neurosci. 2020 Nov;48(4):377-386. doi: 10.1007/s10827-020-00766-1. Epub 2020 Oct 15. J Comput Neurosci. 2020. PMID: 33063225
-
The singularly perturbed Hodgkin-Huxley equations as a tool for the analysis of repetitive nerve activity.J Math Biol. 1990;28(2):177-95. doi: 10.1007/BF00163144. J Math Biol. 1990. PMID: 2319211
-
Low-dimensional models of single neurons: a review.Biol Cybern. 2023 Jun;117(3):163-183. doi: 10.1007/s00422-023-00960-1. Epub 2023 Apr 15. Biol Cybern. 2023. PMID: 37060453 Review.
Cited by
-
Editorial: New technologies improve maternal and newborn safety.Front Med Technol. 2024 May 30;6:1372358. doi: 10.3389/fmedt.2024.1372358. eCollection 2024. Front Med Technol. 2024. PMID: 38872737 Free PMC article. No abstract available.
-
Electrical wave generation and spatial organization in uterine tissue.J R Soc Interface. 2025 May;22(226):20240638. doi: 10.1098/rsif.2024.0638. Epub 2025 May 14. J R Soc Interface. 2025. PMID: 40364760 Free PMC article.
References
-
- Margara F, Wang ZJ, Levrero-Florencio F, Santiago A, Vázquez M, Bueno-Orovio A, et al.. In-silico human electro-mechanical ventricular modelling and simulation for drug-induced pro-arrhythmia and inotropic risk assessment. Progress in Biophysics and Molecular Biology. 2021;159:58–74. doi: 10.1016/j.pbiomolbio.2020.06.007 - DOI - PMC - PubMed
-
- Fall CP, Marland ES, Wanger JM, Tyson JJ, editors. Computational Cell Biology. 1st ed. Interdisciplinary Applied Mathematics. Springer; New York; 2002.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Research Materials

