Experimental quantum imaging distillation with undetected light

Abstract

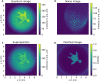
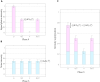
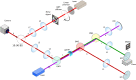
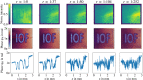
Imaging based on the induced coherence effect makes use of photon pairs to obtain information of an object without detecting the light that probes it. While one photon illuminates the object, only its partner is detected, so no measurement of coincidence events is needed. The sought-after object's information is revealed, observing a certain interference pattern on the detected photon. Here, we demonstrate experimentally that this imaging technique can be made resilient to noise. We introduce an imaging distillation approach based on the interferometric modulation of the signal of interest. We show that our scheme can generate a high-quality image of an object even against noise levels up to 250 times the actual signal of interest. We also include a detailed theoretical explanation of our findings.

Fig. 1.. Principle of quantum imaging distillation.

We use a quantum imaging distillation protocol to remove a noisy image from a quantum image. (A) The quantum image that we aim to distill. (B) The noise image that is superimposed on the quantum image. (C) The superposition of noise and quantum images. (D) The resulting distilled image from noise.

Fig. 2.. Intensity detected in one camera pixel.

For visualization purposes, we have considered the same mean intensities (chart bars) and variances (error bars) for the signal photon and the noise. In (A), the signal photon intensity (in pink) for different values of δ is presented. This intensity fluctuation allows us to compute the object information using QHUL (35). In (B), the noise intensity (in blue) for the same phases δ is presented. In contrast to the signal intensity, the noise intensity is not affected by the value of δ. In (C), the noise and signal intensities are added. Because the noise intensity does not change, its contribution just sets a higher background. On top of it, signal photon intensity still changes, and the total variance is its previous variance plus the noise variance. Thus, an external source of noise increases the shot noise of QHUL.

Fig. 3.. Setup.

The signal and idler beams (in paths b and c, respectively) are generated by the pump beam in path a interacting with the nonlinear crystal [periodically poled potassium titanyl phosphate (ppKTP)] in the forward direction, while paths e and f represent propagations of the down converted beams generated after the pump beam is reflected back into the crystal by mirror M3 in path d. An object in path c is illuminated with the idler beam in the Fourier plane of the crystal. To create the noise, a laser diode of the same wavelength as the signal photon (910 nm) is used. The signal beam in path e is merged with the noise in path g before reaching the camera with a 10:90 beam splitter (BS). On the detector plane, we obtain the quantum image with lenses L2, L4, and L5, and the noise image with lenses L6 and L7. Different type of noise are created with a linear polarizer and a light diffuser in path g. The linear polarizer controls the pump power of the diode laser. The diffuser that consists on a rotating ground glass plate produces a speckle pattern of the noise source. The speed of the rotation is controlled through the glass plate motor interface.

Fig. 4.. Resilience to different noise intensities.

In the top row, the superpositions of quantum (IOF letters) and classical (square shape) images are shown. The ratio between their mean intensities is stated on top of each image. In the middle row, the experimental results for our distillation technique through QHUL are presented. In the last row, a transverse cut of the distilled images is presented. We observe that, while the noise intensity increases, the phase estimation diminishes.

Fig. 5.. Distillation phase variance affected by noise variance.

A light diffuser with four different rotation speeds is used to change the properties of the noise illumination; see supplementary text D. The different noise configurations are represented by different colors and symbols; see inset. Data points represent the experimental phase values obtained for different noise variances, and dashed lines represent their fits. A theoretical black solid line representing a Poissonian noise is also included. In all configurations, we observed that a higher noise variance increases the phase inaccuracy in QHUL. We also corroborate that the phase sensitivity is linearly dependent with the noise variance; for more details, see supplementary text F.

Fig. 6.. Simulated resilience limits.

To find the limits of our technique, we have simulated a Poisonnian source of noise superimposed on our quantum image. The first row shows distilled images for different ratios stated above them. The second row shows a transverse cut of distilled images on top. The simulations show that our technique should be able to work at noise levels beyond 1000 times the quantum signal.