The seasons within: a theoretical perspective on photoperiodic entrainment and encoding

Abstract

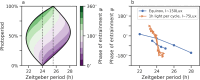
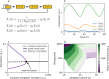
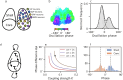
Circadian clocks are internal timing devices that have evolved as an adaption to the omnipresent natural 24 h rhythmicity of daylight intensity. Properties of the circadian system are photoperiod dependent. The phase of entrainment varies systematically with season. Plastic photoperiod-dependent re-arrangements in the mammalian circadian core pacemaker yield an internal representation of season. Output pathways of the circadian clock regulate photoperiodic responses such as flowering time in plants or hibernation in mammals. Here, we review the concepts of seasonal entrainment and photoperiodic encoding. We introduce conceptual phase oscillator models as their high level of abstraction, but, yet, intuitive interpretation of underlying parameters allows for a straightforward analysis of principles that determine entrainment characteristics. Results from this class of models are related and discussed in the context of more complex conceptual amplitude-phase oscillators as well as contextual molecular models that take into account organism, tissue, and cell-type-specific details.

Keywords: Circadian clock; Coupling; Mathematical modeling; Photoperiodic encoding; Seasonality; Synchronization.

Fig. 1

Weak zeitgebers or strong clocks lead to a large phase variability. a Arnold tongue based on phase oscillator model (9) in the parameter plane spanned by the internal free-running period $\tau$ and the amplitude or strength z of the external zeitgeber signal. Color-coded values depict the phase of entrainment $\psi$ as given by Eq. (11). b Experimentally obtained entrainment phases in dependence of the intrinsic free-running period $\tau$ for ruin lizards subject to temperature cycles of different amplitude, i.e., zeitgeber strength. Data have been extracted from Fig. 5 of (Hoffmann 1969) via the WebPlotDigitizer software (Rohatgi 2022). c Arnold tongue in the parameter plane spanned by the period T and amplitude or strength z of the external zeitgeber signal. Color-coded values depict the phase of entrainment $\psi$ as given by Eq. (11). d Experimentally obtained entrainment phases $\psi$ for different species subject to entrainment cycles of different external zeitgeber period T. Species have been categorized into vertebrates (purple lines) as well as plants and unicellular species (brown lines). Please refer to the original publication (Aschoff and Pohl 1978) for the detailed description of the investigated animals and entrainment properties. Data have been extracted from Fig. 2 of (Aschoff and Pohl 1978) via the WebPlotDigitizer software (Rohatgi 2022)

Fig. 2

Arnold onions capture essential features of seasonal entrainment. a Entrainment regions adopt an onion-shaped geometry in the photoperiod-zeitgeber period parameter plane. The tilt of the Arnold onion can be explained by Aschoff’s rule, i.e., the difference between the internal free-running period under constant darkness (photoperiod of $0\%$) and constant light (photoperiod of $100\%$), depicted by vertical dashed lines. Phases of entrainment $\psi$ are color-coded within the region of entrainment. b Experimentally obtained entrainment phase $\psi$ in dependence of the zeitgeber period T for the golden hamster Mesocricetus auratus subject to light–dark cycles with equinoctial (blue) and extremely short (orange) photoperiods. Data have been extracted from Fig. 3 of (Aschoff and Pohl 1978) via the WebPlotDigitizer software (Rohatgi 2022)

Fig. 3

Intrinsic oscillator properties govern seasonal entrainment characteristics. a The Goodwin oscillator is considered a blueprint for models of molecular negative feedback loops. We assume that the (square-wave) zeitgeber signal affects the negative feedback loop by an additive term to the $X_1$-variable. b Example oscillations under free-running conditions for a parameter set that leads to self-sustained oscillations. Same parameters as those underlying Fig. 8 of (Ananthasubramaniam et al. 2020) have been used. c For an increasing constant zeitgeber strength (e.g., constant light of increasing intensity), the system eventually changes its qualitative behavior through a Hopf bifurcation and looses its ability to self-sustain the oscillations. d For large zeitgeber intensities, the bifurcation shown in panel (c) translates into a broad entrainment range under long photoperiods similar to the behavior of damped oscillators. Panels c, d are adapted from Fig. S5a and Fig. 8a of (Ananthasubramaniam et al. 2020), respectively (under CC BY 4.0 license)

Fig. 4

Precision through coupling. a) Phase distributions in large ensembles of clocks can be conveniently visualized on the unit circle of radius 1. The global order parameter $R{e}^{i\mathrm{\Psi }}$, depicted as a blue arrow, conveniently summarizes macroscopic properties of the ensemble. While the phase coherence R is given by the length of the arrow, the average phase $\mathrm{\Psi }$ defines the position of the arrow head similar to the clock hands of a classical mechanical clock. b) The Ott–Antonsen reduction method faithfully reproduces numerical results in an ensemble of uniformly coupled Kuramoto oscillators with unimodally (Cauchy–Lorentz) distributed intrinsic frequencies ${\omega }_i=\frac{2\pi }{{\tau }_i}$. c) For large enough coupling strength, i.e., $K>2\gamma$, oscillators show spontaneous synchronization. Subsequently, the phase coherence increases, i.e., the phase-spread decreases, for increasing coupling strength. Here, a value of $\gamma =0.01$ has been used which approximately corresponds to the experimentally observed standard deviation of $\sigma =1.28h$ for widely dispersed SCN neurons, estimated in the period domain (Herzog et al. 2004). The dashed black line denotes the critical coupling strength $K_c=2\gamma$. d) Representative oscillation phase distribution of PER2::LUC reporter gene expression for individually tracked SCN neurons of cultured SCN slices under control conditions (top) and during application of tetrodotoxin (bottom). Phases are shown in a histogram (left) and at their original positions within the SCN slice (right). Original data have been obtained from (Abel et al. 2016) and oscillation phases have been determined as previously described (Schmal et al. 2018). Arrows in panel (c) point to coupling strength $K\approx 0.028$ and $K\approx 0.200$ that lead to a phase coherence of $R=0.54$ and $R=0.95$ as observed for the exemplary experimental data under control and TTX conditions as shown in panel (d), respectively

Fig. 5

Photoperiodic encoding. a Schematic drawing of region-specific neuropeptide expression within the SCN. b Emergence of spatial phase clustering in cultured SCN slices from mice entrained to extremely long photoperiods of LD20:4. c Histogram of phase values depicted in panel (b) shows a bimodal distribution. Bold and dashed black lines denote a bimodal composite van Mises distribution and the underlying unimodal distributions, respectively, fitted to the histogram data (gray bars). Fitting reveals that the mean phases in the core and shell are separated by ${90}^{\circ }$ after entrainment to light–dark cycles of extremely long photoperiods (LD20:4). Data have been obtained from Evans et al. (2013) and analyzed as previously reported (Schmal et al. 2017). d Schematic drawing of an SCN model, constituted of two groups of interacting oscillators, i.e., core and shell neurons, under the assumption that intracellular oscillators of core and shell neurons follow intrinsic frequency distributions of different mean; see “Materials and Methods” for further model details. e Increasing period differences $\mathrm{\Delta }\tau ={\tau }_C-{\tau }_S$ as well as decreasing coupling strength K between the core (ventral) and shell (dorsal) neurons can lead to an increasing gap between the oscillation phases of core and shell neurons. Color-coded bifurcation diagrams of the Ott–Antonsen reduced system given by Eqs. (6), (7) of the section “Materials and Methods” have been obtained by XPP-Auto. f Ott–Antonsen reduced dynamics faithfully reproduce the behavior of numerical simulations of the full set of equations, compare dashed lines representing the steady-state phases in the core and shell neurons in the low-dimensional Ott–Antonsen reduced representation with the corresponding numerically obtained phase distributions depicted by bar plots. Simulations shown in (f) correspond to the parameter values depicted by the star in (e), i.e., a coupling strength of $K=0.065$, a period difference of $\mathrm{\Delta }\tau =4h$ corresponding to ${\tau }_C=26\text{h}$ and ${\tau }_S=22\text{h}$ as well as a frequency spread of $\gamma =0.01$ as used in Fig. 4b, c