A mathematical theory of relational generalization in transitive inference

Abstract

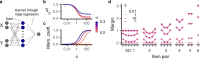
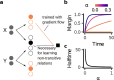
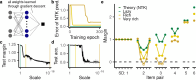
Humans and animals routinely infer relations between different items or events and generalize these relations to novel combinations of items. This allows them to respond appropriately to radically novel circumstances and is fundamental to advanced cognition. However, how learning systems (including the brain) can implement the necessary inductive biases has been unclear. Here we investigated transitive inference (TI), a classic relational task paradigm in which subjects must learn a relation (A > B and B > C) and generalize it to new combinations of items (A > C). Through mathematical analysis, we found that a broad range of biologically relevant learning models (e.g. gradient flow or ridge regression) perform TI successfully and recapitulate signature behavioral patterns long observed in living subjects. First, we found that models with item-wise additive representations automatically encode transitive relations. Second, for more general representations, a single scalar "conjunctivity factor" determines model behavior on TI and, further, the principle of norm minimization (a standard statistical inductive bias) enables models with fixed, partly conjunctive representations to generalize transitively. Finally, neural networks in the "rich regime," which enables representation learning and has been found to improve generalization, unexpectedly show poor generalization and anomalous behavior. We find that such networks implement a form of norm minimization (over hidden weights) that yields a local encoding mechanism lacking transitivity. Our findings show how minimal statistical learning principles give rise to a classical relational inductive bias (transitivity), explain empirically observed behaviors, and establish a formal approach to understanding the neural basis of relational abstraction.

Figure 1:

Transitive inference and behavioral patterns observed in subjects performing this task. a, Example stimuli taken from [31]. An example generalization (B > E) is highlighted. b, In a given trial, the subject is asked to choose between the two presented items. They are rewarded if the chosen item is “larger” according to the underlying hierarchy. This panel depicts a test trial where successful performance would consist in picking the item on the right. c, Schematic of the training and test cases. d, Example accuracy on all training and test cases (in this case by rhesus macaques). Terminal item, symbolic distance, and asymmetry effect are apparent in the plot. In the subsequent figures, we leave off the item pair labels but use the same ordering. Symbolic distance (SD) is the separation in the rank hierarchy. The data is reproduced from [31]. e, Symbolic distance effect with and without a memorization effect (ME). Data without ME reproduced from [31] and data with ME reproduced from [29]. Shaded regions in both panels indicate mean ± one standard error.

Figure 2:

An additive representation yields transitive generalization and the symbolic distance effect. a, Schematic illustration of an additive representation (rep.). The first three orange nodes represent the first item $\left(X\right)$ and the latter three represent the second item $\left(Y\right)$. b, Replacing the second item only results in changes to the highlighted half of the units. c, The readout weights of the model can be grouped into those pertaining to item $X$ and those pertaining to item $Y$. The model’s output can be understood as assigning a “rank” $r\left(X\right)$ and $r\left(Y\right)$ to each item and then computing $r\left(X\right)-r\left(Y\right)$. d, Example of a model’s rank assignment.

Figure 3:

Non-additive representations of TI cases. a, A non-additive representation encodes nonlinear interactions between items. b, A one-hot representation represents each combination of items by a distinct node. c, Representational similarity (cross-correlation) between a subset of trials in a ReLU network with 50,000 units. d, Representational similarity between all possible trials in networks with different numbers of hidden units, organized according to the type of trials. e, The conjunctivity factor characterizes a given representation according to how similarly it represents overlapping trials. Additive representations lie at one end of the spectrum, whereas one-hot representations lie at the other end.

Figure 4:

We analyze the behavior of models having readout weights trained with norm minimization. a, Schematic illustration of the setup. b, Norm minimization implements a useful inductive bias for generalization to nearby data points. On categorization tasks, it determines the hyperplane separating the two categories with the maximal margin. c, Intuitively, a partly conjunctive representation is given by an item-wise representation of $X$ and $Y$ concatenated with a fully conjunctive representation of $X$ and $Y$. The readout from the item-wise representations computes a rank for each item that transfers to overlapping pairs. The readout from the fully conjunctive representation memorizes a response to a given pair and does not transfer to overlapping pairs. Because norm minimization encourages distributed weights, it finds a solution that partly uses the item-wise representation and hence computes a rank. This leads to transitive generalization. d,e, The emergent rank representation at the end of training (Eq. 2) for (d) seven items and different values for $\alpha$; and (e) $\alpha =0.1$ and different numbers of items. f, For seven items and different values for $\alpha$, the corresponding margin for all trials. Item pairs are arranged by their position in the hierarchy, as in Fig. 1e.

Figure 5:

TI behavior for models with a fixed representation and readout weights trained using regularized regression. a, Illustration of the setup. b,c, The (b) effective conjunctivity factor and (c) memorization coefficient as a function of the inverse regularization coefficient c. d, Generalization behavior for $\alpha =0.1$ and different values of $c$. The margins overall become larger as c increases.

Figure 6:

Behavior of models trained with readout weights trained through gradient flow on transverse patterning. a, Learning a non-transitive relation requires a conjunctive component. b, Margin over time for different values of $\alpha$. c, Halftime, i.e. time until the model reaches a margin of 0.5, as a function of the conjunctivity factor $\alpha$.

Figure 7:

TI behavior in deep neural networks with modifiable representations. We considered twenty instances of a network with a ReLU nonlinearity and one hidden layer with 50,000 units, trained using mean squared error. Appendix S2.5 details other architectures, nonlinearities, and objective functions. Shaded regions indicate mean ± one standard deviation. (Note that some of the behaviors have sufficiently small variance that this shaded region may be invisible.) a, Illustration of network training. In contrast to the previous setups, the hidden layer weights were also trained using backpropagation. b, The mean squared error of the prediction made by the neural tangent kernel (NTK) at three different initialization scales (lazy: 1; rich: 10⁻³; very rich: 10⁻¹⁶). c,d, The (c) average test margin and (d) test accuracy as a function of initialization scale. The colored lines highlight the three representative values analyzed in more detail in panels b and e. e, TI performance according to our NTK-based prediction as well as of networks trained with backpropagation at the three representative scales.

Figure 8:

A mechanistic analysis of the rich regime’s inductive bias. All plots show the mean ± standard deviation across twenty random initializations. Standard deviation is too small to be visible. a, ${\ell }_2$-norm of of all weights in the fully trained networks as a function of initialization scale. The rich regime yields much smaller norm. b, Inertia (i.e. proportion of explained variance) as a function of the number of clusters, for the lazy and rich network. Six clusters only leave 0.001% of the variance unexplained. c, The empirical network is therefore described by a network with six units, three with positive and three with negative responses. The right panels show the weights of the different units and the bottom panel shows how each units responds to the different training trials. Only units with positive readout weights are shown; the units with negative readout weights have the same structure but with Item 1 and 2 reversed. d, Analogous depiction of the hand-constructed network, which has four units. e, The rank network only has two units, but they span a much wider range. f, Weight norm of the empirical, hand-constructed, and rank network as a function of the number of items. The rank network has a much larger ${\ell }_2$-norm, whereas the norm of the empirical network is similar to that of the hand-constructed network.