Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Aug 16;9(9):e19059.
doi: 10.1016/j.heliyon.2023.e19059. eCollection 2023 Sep.

Dual core processors: Coupled queues: Transient performance evaluation

Shaik Salma  1 , Garimella Ramamurthy  1
Affiliations

Dual core processors: Coupled queues: Transient performance evaluation

Shaik Salma et al. Heliyon. .

Abstract

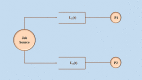
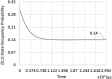
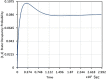
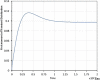
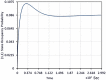
High-Performance Computing (HiPC) systems routinely employ multi/many - core processors. Specifically, dual - core processors find many applications in pervasive computing devices. Dual-core processors employ buffers for queueing the incoming jobs. Traditionally, the queues at the processors are assumed to be independent and the queueing system is analyzed in equilibrium for tractability purposes. Queues are modeled using Continuous Time Markov Chains (CTMC's) and the equilibrium performance measures are determined to analyze as well as design the queueing systems. In most interesting cases, the incoming jobs are routed to the queues using the Join the Shortest Queue (JSQ) policy. Thus, with such an adaptive routing algorithm, the two queues are evidently coupled and are not statistically independent. Hence traditional equilibrium performance evaluation doesn't provide realistic performance measures. In this research paper, the two queues associated with buffers in dual-core processors are considered to be coupled. The Coupled Queues are modeled using a Quasi - Birth - and - Death (QBD) process. Using traditional results related to QBD processes, equilibrium performance measures are determined. More interestingly, we demonstrate the tractability of the computation of transient probability distribution of a QBD process. In the research literature, transient analysis of the QBD process was shown to be tractable in the Laplace transform domain. But in this research paper, we prove that the matrix exponential eQt arising in transient analysis (where Q is the generator matrix of the QBD process) can be computed directly in the time domain rendering efficient transient analysis of QBD process. Using the transient probability mass function of queue length, estimation of transient performance measures such as expected queue length, average delay, and tail distribution can be determined. Further, optimal adaptive routing algorithms for coupled queues can be designed.

Keywords: Coupled Queues; Markov Chain; Matrix Exponential; Multi-core Processor; Transient Analysis.

PubMed Disclaimer

Conflict of interest statement

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Figures

Figure 1
Figure 1
Coupled queues that are statistically dependent.
Figure 2
Figure 2
Time dependent probability evolution for QBD that starts in (0,1) state with probability 0.31 (i.e. Queue 2 has one job in the queue at time 0 and no jobs in queue 1).
Figure 3
Figure 3
Probability as a function of time that the process is in the state (1,1). (At time 0, the probability that queues 1 and 2 have one job is zero.).
Figure 4
Figure 4
Time varying Average Queue length of Queue, 1 (for different initial conditions).
Figure 5
Figure 5
The tail distribution of QBD Modeling coupled queues (probability that queue length in queue 1 is more than 1).
See this image and copyright information in PMC

References

    1. Adan I.J.B.F., Wessels J., Zijm W.H.M. Analysis of the asymmetric shortest queue problem. Queueing Syst. 1991;8:1–58. doi: 10.1007/BF02412240. - DOI
    1. Ephremides A., Varaiya P., Walrand J. A simple dynamic routing problem. IEEE Trans. Autom. Control. 1980;AC-25(4):690–693. doi: 10.1109/TAC.1980.1102445. - DOI
    1. Gaver D.P., Jacobs P.A., Latouche G. Finite birth-and-death models in randomly changing environments. Adv. Appl. Probab. 1984;16:715–731. doi: 10.2307/1427338. - DOI
    1. Lin H.C., Raghavendra C.S. Proceedings of the 12th Int'l Conference on Distributed Computing Systems. June 1992. An analysis of the join the shortest queue (JSQ) policy; pp. 362–366. - DOI
    1. Rama Murthy G. Purdue University; 1989. Transient and equilibrium analysis of computer networks: finite memory and matrix geometric recursions. Ph.D. Thesis. Easy Chair Preprint No. 490.

LinkOut - more resources