Facing the phase problem
- PMID: 37668214
- PMCID: PMC10478523
- DOI: 10.1107/S2052252523006449
Facing the phase problem
Abstract
The marvel of X-ray crystallography is the beauty and precision of the atomic structures deduced from diffraction patterns. Since these patterns record only amplitudes, phases for the diffracted waves must also be evaluated for systematic structure determination. Thus, we have the phase problem as a central complication, both intellectually for the field and practically so for many analyses. Here, I discuss how we - myself, my laboratory and the diffraction community - have faced the phase problem, considering the evolution of methods for phase evaluation as structural biology developed to the present day. During the explosive growth of macromolecular crystallography, practice in diffraction analysis evolved from a universal reliance on isomorphous replacement to the eventual domination of anomalous diffraction for de novo structure determination. As the Protein Data Bank (PDB) grew and familial relationships among proteins became clear, molecular replacement overtook all other phasing methods; however, experimental phasing remained essential for molecules without obvious precedents, with multi- and single-wavelength anomalous diffraction (MAD and SAD) predominating. While the mathematics-based direct methods had proved to be inadequate for typical macromolecules, they returned to crack substantial selenium substructures in SAD analyses of selenomethionyl proteins. Native SAD, exploiting the intrinsic S and P atoms of biomolecules, has become routine. Selenomethionyl SAD and MAD were the mainstays of structural genomics efforts to populate the PDB with novel proteins. A recent dividend has been paid in the success of PDB-trained artificial intelligence approaches for protein structure prediction. Currently, molecular replacement with AlphaFold models often obviates the need for experimental phase evaluation. For multiple reasons, we are now unfazed by the phase problem. Cryo-EM analysis is an attractive alternative to crystallography for many applications faced by today's structural biologists. It simply finesses the phase problem; however, the principles and procedures of diffraction analysis remain pertinent and are adopted in single-particle cryo-EM studies of biomolecules.
Keywords: anomalous diffraction; density modification; direct methods; isomorphous replacement; molecular replacement.
open access.
Figures

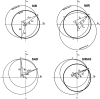
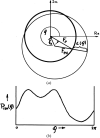

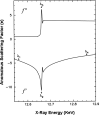
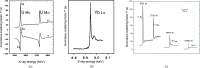









Similar articles
-
Robust structural analysis of native biological macromolecules from multi-crystal anomalous diffraction data.Acta Crystallogr D Biol Crystallogr. 2013 Jul;69(Pt 7):1314-32. doi: 10.1107/S0907444913001479. Epub 2013 Jun 13. Acta Crystallogr D Biol Crystallogr. 2013. PMID: 23793158 Free PMC article.
-
Anomalous diffraction in crystallographic phase evaluation.Q Rev Biophys. 2014 Feb;47(1):49-93. doi: 10.1017/S0033583514000018. Q Rev Biophys. 2014. PMID: 24726017 Free PMC article. Review.
-
Structures from anomalous diffraction of native biological macromolecules.Science. 2012 May 25;336(6084):1033-7. doi: 10.1126/science.1218753. Science. 2012. PMID: 22628655 Free PMC article.
-
Multi-crystal anomalous diffraction for low-resolution macromolecular phasing.Acta Crystallogr D Biol Crystallogr. 2011 Jan;67(Pt 1):45-59. doi: 10.1107/S0907444910046573. Epub 2010 Dec 16. Acta Crystallogr D Biol Crystallogr. 2011. PMID: 21206061 Free PMC article.
-
Contemporary Use of Anomalous Diffraction in Biomolecular Structure Analysis.Methods Mol Biol. 2017;1607:377-399. doi: 10.1007/978-1-4939-7000-1_16. Methods Mol Biol. 2017. PMID: 28573582 Free PMC article. Review.
Cited by
-
A note on the Hendrickson-Lattman phase probability distribution and its equivalence to the generalized von Mises distribution.J Appl Crystallogr. 2024 Feb 16;57(Pt 2):492-498. doi: 10.1107/S1600576724000311. eCollection 2024 Apr 1. J Appl Crystallogr. 2024. PMID: 38596730 Free PMC article.
-
Systematic enhancement of protein crystallization efficiency by bulk lysine-to-arginine (KR) substitution.Protein Sci. 2024 Mar;33(3):e4898. doi: 10.1002/pro.4898. Protein Sci. 2024. PMID: 38358135 Free PMC article.
-
A modified phase-retrieval algorithm to facilitate automatic de novo macromolecular structure determination in single-wavelength anomalous diffraction.IUCrJ. 2024 Jul 1;11(Pt 4):587-601. doi: 10.1107/S2052252524004846. IUCrJ. 2024. PMID: 38904547 Free PMC article.
-
Commentary on `Facing the phase problem' by Wayne Hendrickson.IUCrJ. 2023 Sep 1;10(Pt 5):555-556. doi: 10.1107/S2052252523007340. IUCrJ. 2023. PMID: 37615300 Free PMC article.
References
-
- Abbe, E. (1873). Arch. Mikrosk. Anat. 9, 413–468.
-
- Abrahams, J. P. & Leslie, A. G. W. (1996). Acta Cryst. D52, 30–42. - PubMed
-
- Als-Nielsen, J. & McMorrow, D. (2011). Elements of Modern X-ray Physics, 2nd ed. Chichester: John Wiley & Sons.
-
- Assur Sanghai, Z., Liu, Q., Clarke, O. B., Belcher-Dufrisne, M., Wiriyasermkul, P., Giese, M. H., Leal-Pinto, E., Kloss, B., Tabuso, S., Love, J., Punta, M., Banerjee, S., Rajashankar, K. R., Rost, B., Logothetis, D., Quick, M., Hendrickson, W. A. & Mancia, F. (2018). eLife, 7, e27829. - PMC - PubMed
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

