Semi-supervised mixture multi-source exchangeability model for leveraging real-world data in clinical trials

Abstract

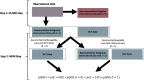
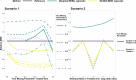
The traditional trial paradigm is often criticized as being slow, inefficient, and costly. Statistical approaches that leverage external trial data have emerged to make trials more efficient by augmenting the sample size. However, these approaches assume that external data are from previously conducted trials, leaving a rich source of untapped real-world data (RWD) that cannot yet be effectively leveraged. We propose a semi-supervised mixture (SS-MIX) multisource exchangeability model (MEM); a flexible, two-step Bayesian approach for incorporating RWD into randomized controlled trial analyses. The first step is a SS-MIX model on a modified propensity score and the second step is a MEM. The first step targets a representative subgroup of individuals from the trial population and the second step avoids borrowing when there are substantial differences in outcomes among the trial sample and the representative observational sample. When comparing the proposed approach to competing borrowing approaches in a simulation study, we find that our approach borrows efficiently when the trial and RWD are consistent, while mitigating bias when the trial and external data differ on either measured or unmeasured covariates. We illustrate the proposed approach with an application to a randomized controlled trial investigating intravenous hyperimmune immunoglobulin in hospitalized patients with influenza, while leveraging data from an external observational study to supplement a subgroup analysis by influenza subtype.

Keywords: Bayesian model averaging; Causal inference; Influenza; Propensity scores; Real-world data.

Fig. 1

Overview of SS-MIX–MEM approach.

Fig. 2

Simulations figures. Scenario 1: the “ideal scenario” where the RCT and observational populations are identical, there is no residual bias. Scenario 2: we vary the proportion of observational study individuals from the RCT population. Scenario 3: we introduce residual differences between the RCT and the representative subgroup.

Fig. 3

FLU-IVIG and FLU 003 application results. Subtype A: All methods produce similar null results with 95% confidence/credible intervals (CIs) for the OR including 1. For all borrowing approaches, ESSS values are greater than 0 and 95% CIs are smaller than a reference model indicating that we gain precision from borrowing. Subtype B: All methods have similar results with OR estimates well below 1 and none of the 95% CIs for the OR including 1. The borrowing approaches do not leverage the FLU 003 data illustrated by ESSS values around 0.

Fig. 4

Borrowing on both arms simulations results. Scenario 1: there is no bias introduced, confounding is introduced via the treated and control arms mixing parameters, which both vary between 0 and 1. Note that the x-axis is the true mixing parameter of the treated individuals in the observational data and the linetype is the true mixing parameter of the control individuals in the observational data. Scenario 2: the mixing parameter for the treated and control arms is either both 0.5 or both 1, residual bias varies between –2 and 2 for the treated arm observational data, the control arm has no residual bias. Note that the x-axis is the log OR between the treated individuals in the observational data and the treated individuals in the trial.