Comparing the Accuracy of the Kane, Barrett Universal II, Hill-Radial Basis Function, Emmetropia Verifying Optical, and Ladas Super Formula Intraocular Lens Power Calculation Formulas

Abstract

Purpose: To assess the accuracy of five new-generation intraocular lens (IOL) power formulas: Barrett Universal II (BUII), Emmetropia Verifying Optical (EVO) Formula, Hill-Radial Basis Function (Hill-RBF), Kane Formula, and Ladas Super Formula (LSF).

Patients and methods: This is a retrospective single-surgeon study from a refractive clinic and clinical research center in Draper, UT, USA. The primary outcome measures were mean absolute error (MAE) and median absolute error (MedAE). Secondary outcome measures were the standard deviation (SD) of each formula's refractive prediction errors (RPE) and the percentage of eyes within ±0.50D. Refractive predictions were compared to the postoperative spherical equivalent to determine the RPE for each formula. RPEs were optimized, and MAE, MedAE, SD of the AME, and percent of eyes achieving RPEs within the specified ranges of ±0.125 D, ±0.25 D, ±0.50 D, ±0.75 D, ±1.0 D were calculated. Subgroup analysis between different axial lengths was attempted but yielded insufficient statistical power to draw meaningful conclusions.

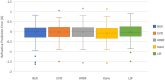
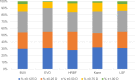
Results: A total of 103 eyes of 103 patients were included in our study after applying inclusion and exclusion criteria to 606 eyes from 2019 to 2021. Formulas ranked in ascending order by MAE were Kane, EVO, BUII, Hill-RBF, and LSF. The ascending rankings of MedAE were Kane, BUII, Hill-RBF, EVO, Ladas. Kane had a significantly lower MAE than Hill-RBF (p<0.001). EVO had the lowest SD of AMEs and the highest percentage of eyes within ±0.50 D. According to heteroscedastic testing, EVO also had a statistically significant lower SD than Hill-RBF.

Conclusion: Kane was the most accurate formula in terms of MAE and MedAE. EVO and BUII achieved marginally higher MAEs than Kane, suggesting these three formulas are comparable in performance. With the exception EVO and Hill-RBF, the heteroscedastic test yielded no significant differences in SD between the formulas. Although there were multiple statistically significant differences between the formulas in terms of MAE, MedAE, and SD, these differences may not be appreciable clinically. Lastly, there were no statistically significant differences in the percent of eyes with RPEs within ±0.50 D, suggesting similar clinical performance between formulas.

Keywords: CLE; IOL power formulas; RLE; cataract surgery; clear lens extraction; new generation IOL formulas; refractive lens exchange; refractive surgery.

Figure 1

Box and whisker plot showing the initial distribution and outliers of each formula’s refractive prediction errors prior to optimization (n=103).

Figure 2

Percentage of eyes within prediction errors of ±0.125 D, ±0.25 D, ±0.5 D, ±0.75 D, ± 1.00 D (n=103).