Treating Semiempirical Hamiltonians as Flexible Machine Learning Models Yields Accurate and Interpretable Results
- PMID: 37705220
- PMCID: PMC10536991
- DOI: 10.1021/acs.jctc.3c00491
Treating Semiempirical Hamiltonians as Flexible Machine Learning Models Yields Accurate and Interpretable Results
Abstract
Quantum chemistry provides chemists with invaluable information, but the high computational cost limits the size and type of systems that can be studied. Machine learning (ML) has emerged as a means to dramatically lower the cost while maintaining high accuracy. However, ML models often sacrifice interpretability by using components such as the artificial neural networks of deep learning that function as black boxes. These components impart the flexibility needed to learn from large volumes of data but make it difficult to gain insight into the physical or chemical basis for the predictions. Here, we demonstrate that semiempirical quantum chemical (SEQC) models can learn from large volumes of data without sacrificing interpretability. The SEQC model is that of density-functional-based tight binding (DFTB) with fixed atomic orbital energies and interactions that are one-dimensional functions of the interatomic distance. This model is trained to ab initio data in a manner that is analogous to that used to train deep learning models. Using benchmarks that reflect the accuracy of the training data, we show that the resulting model maintains a physically reasonable functional form while achieving an accuracy, relative to coupled cluster energies with a complete basis set extrapolation (CCSD(T)*/CBS), that is comparable to that of density functional theory (DFT). This suggests that trained SEQC models can achieve a low computational cost and high accuracy without sacrificing interpretability. Use of a physically motivated model form also substantially reduces the amount of ab initio data needed to train the model compared to that required for deep learning models.
Conflict of interest statement
The authors declare no competing financial interest.
Figures
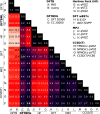
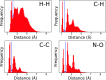
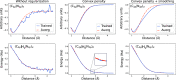
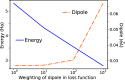
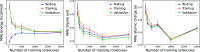
 where σ is the standard deviation
of the errors calculated separately for the training, validation,
and testing values.
where σ is the standard deviation
of the errors calculated separately for the training, validation,
and testing values.
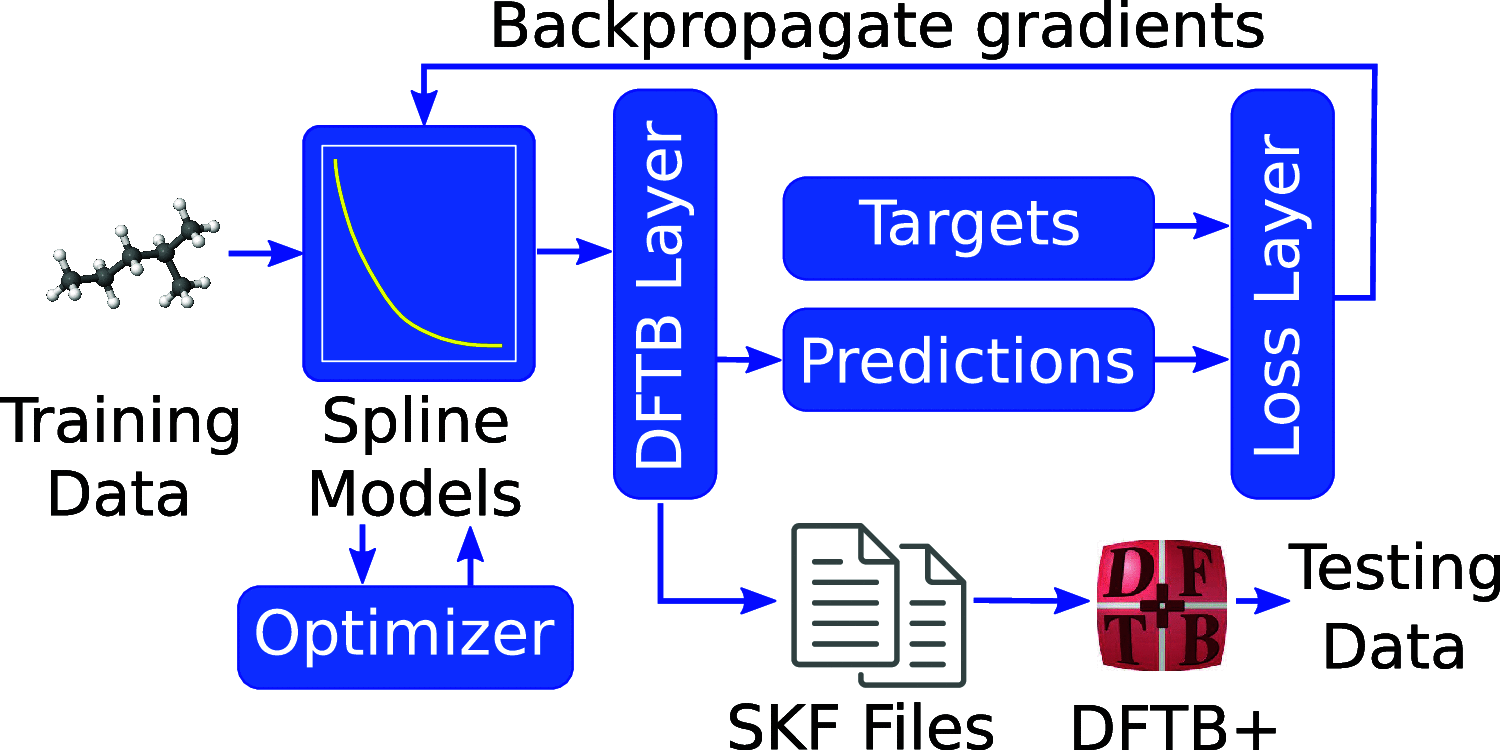
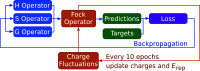
Similar articles
-
Deep learning of dynamically responsive chemical Hamiltonians with semiempirical quantum mechanics.Proc Natl Acad Sci U S A. 2022 Jul 5;119(27):e2120333119. doi: 10.1073/pnas.2120333119. Epub 2022 Jul 1. Proc Natl Acad Sci U S A. 2022. PMID: 35776544 Free PMC article.
-
Calculations on noncovalent interactions and databases of benchmark interaction energies.Acc Chem Res. 2012 Apr 17;45(4):663-72. doi: 10.1021/ar200255p. Epub 2012 Jan 6. Acc Chem Res. 2012. PMID: 22225511 Review.
-
Accurate Many-Body Repulsive Potentials for Density-Functional Tight Binding from Deep Tensor Neural Networks.J Phys Chem Lett. 2020 Aug 20;11(16):6835-6843. doi: 10.1021/acs.jpclett.0c01307. Epub 2020 Aug 7. J Phys Chem Lett. 2020. PMID: 32787209
-
Ab Initio Calculations for Molecule-Surface Interactions with Chemical Accuracy.Acc Chem Res. 2019 Dec 17;52(12):3502-3510. doi: 10.1021/acs.accounts.9b00506. Epub 2019 Nov 25. Acc Chem Res. 2019. PMID: 31765121
-
Performance Assessment of Universal Machine Learning Interatomic Potentials: Challenges and Directions for Materials' Surfaces.ACS Appl Mater Interfaces. 2025 Mar 5;17(9):13111-13121. doi: 10.1021/acsami.4c03815. Epub 2024 Jul 11. ACS Appl Mater Interfaces. 2025. PMID: 38990833 Review.
Cited by
-
OpenMM 8: Molecular Dynamics Simulation with Machine Learning Potentials.J Phys Chem B. 2024 Jan 11;128(1):109-116. doi: 10.1021/acs.jpcb.3c06662. Epub 2023 Dec 28. J Phys Chem B. 2024. PMID: 38154096 Free PMC article.
-
Cross-disciplinary perspectives on the potential for artificial intelligence across chemistry.Chem Soc Rev. 2025 Jun 3;54(11):5433-5469. doi: 10.1039/d5cs00146c. Chem Soc Rev. 2025. PMID: 40278836 Free PMC article. Review.
-
Efficient Parameterization of Density Functional Tight-Binding for 5f-Elements: A Th-O Case Study.J Chem Theory Comput. 2024 Jul 23;20(14):5923-5936. doi: 10.1021/acs.jctc.4c00145. Epub 2024 Jul 11. J Chem Theory Comput. 2024. PMID: 38990696 Free PMC article.
-
Data Generation for Machine Learning Interatomic Potentials and Beyond.Chem Rev. 2024 Dec 25;124(24):13681-13714. doi: 10.1021/acs.chemrev.4c00572. Epub 2024 Nov 21. Chem Rev. 2024. PMID: 39572011 Free PMC article. Review.
References
-
- Scuseria G. E. Comparison of coupled-cluster results with a hybrid of Hartree-Fock and density functional theory. J. Chem. Phys. 1992, 97, 7528–7530. 10.1063/1.463977. - DOI
-
- Gruber T.; Liao K.; Tsatsoulis T.; Hummel F.; Grüneis A. Applying the Coupled-Cluster Ansatz to Solids and Surfaces in the Thermodynamic Limit. Phys. Rev. X 2018, 8, 02104310.1103/PhysRevX.8.021043. - DOI
LinkOut - more resources
Full Text Sources

