Neuromusculoskeletal model-informed machine learning-based control of a knee exoskeleton with uncertainties quantification

Abstract

Introduction: Research interest in exoskeleton assistance strategies that incorporate the user's torque capacity is growing rapidly. However, the predicted torque capacity from users often includes uncertainty from various sources, which can have a significant impact on the safety of the exoskeleton-user interface.

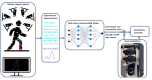
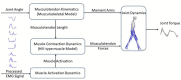
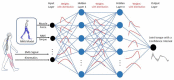
Methods: To address this challenge, this paper proposes an adaptive control framework for a knee exoskeleton that uses muscle electromyography (EMG) signals and joint kinematics. The framework predicted the user's knee flexion/extension torque with confidence bounds to quantify the uncertainty based on a neuromusculoskeletal (NMS) solver-informed Bayesian Neural Network (NMS-BNN). The predicted torque, with a specified confidence level, controlled the assistive torque provided by the exoskeleton through a TCP/IP stream. The performance of the NMS-BNN model was also compared to that of the Gaussian process (NMS-GP) model.

Results: Our findings showed that both the NMS-BNN and NMS-GP models accurately predicted knee joint torque with low error, surpassing traditional NMS models. High uncertainties were observed at the beginning of each movement, and at terminal stance and terminal swing in self-selected speed walking in both NMS-BNN and NMS-GP models. The knee exoskeleton provided the desired assistive torque with a low error, although lower torque was observed during terminal stance of fast walking compared to self-selected walking speed.

Discussion: The framework developed in this study was able to predict knee flexion/extension torque with quantifiable uncertainty and to provide adaptive assistive torque to the user. This holds significant potential for the development of exoskeletons that provide assistance as needed, with a focus on the safety of the exoskeleton-user interface.

Keywords: data-driven biomechanical models; inverse dynamics; machine learning; neuromusculoskeletal modeling; uncertainty quantification.

Figure 1

Schematic of the adaptive control framework for a knee exoskeleton based on an NMS solver-informed BNN (NMS-BNN) model. The inputs to the NMS-BNN include observed muscle signals and joint angles, as well as physical features derived from the NMS solver such as individual muscle force and joint torque. The NMS-BNN outputs knee joint torque with uncertainty quantification in the form of confidence bounds. The predicted torque with a specified confidence level is then used to control the assistive torque provided by the knee exoskeleton through a TCP/IP data stream.

Figure 2

Experimental setup: subjects equipped with EMG sensors and markers, performed movements in an instrumented motion lab.

Figure 3

Schematic structure of an EMG-driven neuromusculoskeletal model with four components: the musculotendon kinematics component calculates musculotendon lengths and moment arms; the muscle activation dynamics component uses the EMG information to compute muscle activation; the muscle contraction dynamics component, predicts musculotendon force using musculotendon length and muscle activation based on a Hill-type muscle model; and finally, the joint dynamics component computes joint torques with musculotendon forces and moment arms as inputs.

Figure 4

Architecture for the NMS-BNN model. The NMS-BNN models consist of an input neural layer, 3 hidden layers, and an output neural layer. The inputs, $\text{x}={\left[x_1,x_2,\dots ,x_m\right]}^T$ where m = 21, were augmented with two types of features: (1) Muscle EMG signals and joint kinematics from a 3D motion capture system, and (2) Physical features such as muscle forces and NMS torque from an underlying NMS solver, to increase the model's accuracy by providing more information about the system being modeled. Each hidden layer has 40 neurons. The estimated knee torque with uncertainties bound was determined in the output layer. Weights are treated as probability distributions rather than as single-point estimates as in standard neural networks. These distributions are used to reflect the uncertainty in weights and predictions.

Figure 5

The distributions of NRMSE between estimated and measured/actual knee joint torques across subjects in NMS, NMS-GP, and NMS-BNN models during five daily activities. The violin plots depict the probability distributions of NRMSE using kernel density plots, and the box plots represent the minimum, lower quartile, median, upper quartile, and maximum values of NRMSE. A significant difference between any two models is indicated by an asterisk (*), based on paired t-test (for normally distributed data) or Wilcoxon signed-rank test (for non-normally distributed data) with Bonferroni correction.

Figure 6

The distributions of RMSE between estimated and measured/actual knee joint torques across subjects in NMS, NMS-GP, and NMS-BNN models during five daily activities. The violin plots depict the probability distributions of NRMSE using kernel density plots, and the box plots represent the minimum, lower quartile, median, upper quartile, and maximum values of NRMSE. A significant difference between any two models is indicated by an asterisk (*), based on paired t-test (for normally distributed data) or Wilcoxon signed-rank test (for non-normally distributed data) with Bonferroni correction.

Figure 7

(A) The uncertainty quantification of predicted knee joint torque by the NMS-GP and NMS-BNN models across subjects during five daily activities, as the mean ± 1 standard deviation of all subjects. The uncertainty was quantified using a 95% confidence level, meaning that there is a 95% probability that the true value falls within the predicted interval. A high uncertainty value indicates low confidence in the prediction. (B) One example of measured knee flex/extension torques (Nm/kg) by inverse dynamics (ID) and predicted values by both NMS and NMS-GP models during five daily activities. The standard deviation in the NMS-GP models highlights the uncertainties from the expected mean value. (C) One example of predicted knee flex/extension torques by NMS-BNN models was presented and compared with the same example from ID and NMS models in (B). The standard deviation in the NMS-BNN models also highlights the uncertainties from the expected mean value.

Figure 8

The tracking error of the knee exoskeleton's assistive torque provided by the adaptive control framework during five daily activities, presented as (A) NRMSE and (B) RMSE. The violin plots illustrate the probability distributions of prediction error through kernel density plots, and the box plots depict the minimum, first quartile, median, third quartile, and maximum values of the prediction error.

Figure 9

One example of the desired and actual assistive torque provided by the knee exoskeleton during five daily activities.