Coarse-Grained Modeling Using Neural Networks Trained on Structural Data

Abstract

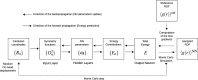
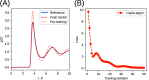
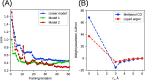
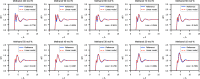
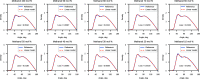
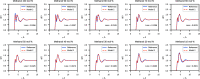
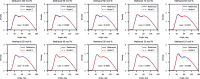
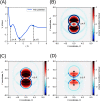
We propose a method of bottom-up coarse-graining, in which interactions within a coarse-grained model are determined by an artificial neural network trained on structural data obtained from multiple atomistic simulations. The method uses ideas of the inverse Monte Carlo approach, relating changes in the neural network weights with changes in average structural properties, such as radial distribution functions. As a proof of concept, we demonstrate the method on a system interacting by a Lennard-Jones potential modeled by a simple linear network and a single-site coarse-grained model of methanol-water solutions. In the latter case, we implement a nonlinear neural network with intermediate layers trained by atomistic simulations carried out at different methanol concentrations. We show that such a network acts as a transferable potential at the coarse-grained resolution for a wide range of methanol concentrations, including those not included in the training set.

Figure 1

Training algorithm outline.

Figure 2

Atomistic and coarse-grained representations of methanol–water mixtures. Pure methanol at the atomistic resolution (A) and the coarse-grained resolution (C) and the methanol–water mixture (20 mol % CH₃OH) at the atomistic resolution (B) and the coarse-grained resolution (D).

Figure 3

(A) Comparison of the reference RDF and the RDF sampled with NN for liquid argon at 95 K and (B) loss convergence for the liquid argon at 95 K.

Figure 4

(A) Convergence of the loss function for the CG methanol models. (B) Optimized linear NN weights for the methanol–water system (blue) and for the liquid argon system (orange), as a function of G² symmetry function r_s parameter.

Figure 5

Comparison of the reference RDF and the RDF sampled with the linear model for CG water–methanol mixtures.

Figure 6

Comparison of the reference angular distribution and the distribution sampled with the linear model for CG water–methanol mixtures.

Figure 7

Comparison of the reference RDF and the RDF sampled with Model 2 for CG water–methanol mixtures.

Figure 8

Comparison of the reference angular distribution and the distribution sampled with Model 2 for CG water–methanol mixtures.

Figure 9

Comparison of the reference RDF and the RDF sampled with the IMC effective potential trained on 40 mol % methanol.

Figure 10

Comparison of the radial distribution function loss values obtained for Model 2 and three of the best IMC models.

Figure 11

Illustration of the three-body component of the ANN potential trained for the nonlinear CG methanol model (Model 1). (A) Pair component of the ANN potential computed as the energy of two CG particles and (B–D) three-body component of the ANN potential computed as the energy difference ΔE⁽³⁾ = E⁽³⁾(1, 2, 3) – E⁽²⁾(1, 2) – E⁽²⁾(2, 3) – E⁽²⁾(1, 2), where E⁽³⁾(1, 2, 3) is the energy of three CG particles and E⁽²⁾(i, j) is the energy of each of the three particle pairs. The three-body component is shown as a density map of the position of the third particle when the first two particles are fixed at distances of 3.4, 4.5, and 6.3 Å, respectively.