A Unified Determinant-Preserving Formulation for Compressible/Incompressible Finite Viscoelasticity
- PMID: 37724292
- PMCID: PMC10505359
- DOI: 10.1016/j.jmps.2023.105312
A Unified Determinant-Preserving Formulation for Compressible/Incompressible Finite Viscoelasticity
Abstract
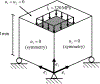
This paper presents a formulation alongside a numerical solution algorithm to describe the mechanical response of bodies made of a large class of viscoelastic materials undergoing arbitrary quasistatic finite deformations. With the objective of having a unified formulation that applies to a wide range of highly compressible, nearly incompressible, and fully incompressible soft organic materials in a numerically tractable manner, the viscoelasticity is described within a Lagrangian setting by a two-potential mixed formulation. In this formulation, the deformation field, a pressure field that ensues from a Legendre transform, and an internal variable of state that describes the viscous part of the deformation are the independent fields. Consistent with the experimental evidence that viscous deformation is a volume-preserving process, the internal variable is required to satisfy the constraint det . To solve the resulting initial-boundary-value problem, a numerical solution algorithm is proposed that is based on a finite-element (FE) discretization of space and a finite-difference discretization of time. Specifically, a Variational Multiscale FE method is employed that allows for an arbitrary combination of shape functions for the deformation and pressure fields. To deal with the challenging non-convex constraint det , a new time integration scheme is introduced that allows to convert any explicit or implicit scheme of choice into a stable scheme that preserves the constraint det identically. A series of test cases is presented that showcase the capabilities of the proposed formulation.
Keywords: Elastomers; Finite deformations; Stabilized finite elements; Stable ODE solvers.
Conflict of interest statement
Declaration of interests The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures





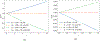



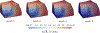
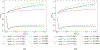

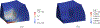
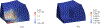
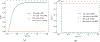
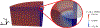


References
-
- Ahn B, Kim J, 2010. Measurement and characterization of soft tissue behavior with surface deformation and force response under large deformations. Medical Image Analysis 14, 138–148. - PubMed
-
- Anand M, Kwack J, Masud A, 2013. A new generalized Oldroyd-B model for blood flow in complex geometries. International Journal of Engineering Science 72, 78–88.
-
- Arnold VI, 1989. Mathematical methods of classical mechanics, 2nd ed, Graduate texts in mathematics. Springer, New York.
-
- Arruda EM, Boyce MC, 1993. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 41, 389–412.
-
- Beatty MF, 2003. An average-stretch full-network model for rubber elasticity. J. Elasticity 70, 65–86.
Grants and funding
LinkOut - more resources
Full Text Sources
