Cluster Formation in Solutions of Polyelectrolyte Rings
- PMID: 37729077
- PMCID: PMC10655244
- DOI: 10.1021/acsnano.3c06083
Cluster Formation in Solutions of Polyelectrolyte Rings
Abstract
We use molecular dynamics simulations to explore concentrated solutions of semiflexible polyelectrolyte ring polymers, akin to the DNA mini-circles, with counterions of different valences. We find that the assembly of rings into nanoscopic cylindrical stacks is a generic feature of the systems, but the morphology and dynamics of such a cluster can be steered by the counterion conditions. In general, a small addition of trivalent ions can stabilize the emergence of clusters due to the counterion condensation, which mitigates the repulsion between the like-charged rings. Stoichiometric addition of trivalent ions can even lead to phase separation of the polyelectrolyte ring phase due to the ion-bridging effects promoting otherwise entropically driven clustering. On the other hand, monovalent counterions cause the formation of stacks to be re-entrant with density. The clusters are stable within a certain window of concentration, while above the window the polyelectrolytes undergo an osmotic collapse, disfavoring ordering. The cluster phase exhibits characteristic cluster glass dynamics with arrest of collective degrees of freedom but not the self-ones. On the other hand, the collapsed phase shows arrest on both the collective and single level, suggesting an incipient glass-to-glass transition, from a cluster glass of ring clusters to a simple glass of rings.
Keywords: DNA mini-rings; clustering; molecular dynamics; polyelectrolytes; ring polymers; slow dynamics; threading.
Conflict of interest statement
The authors declare no competing financial interest.
Figures
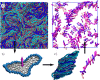
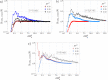

 , or pairs of rings 1 and 2, separated by
at most 0.5Rg,0 plotted for different
densities for the system with monovalent ions only. (c) Weight-weighed
mean aggregation number,
, or pairs of rings 1 and 2, separated by
at most 0.5Rg,0 plotted for different
densities for the system with monovalent ions only. (c) Weight-weighed
mean aggregation number,  , of rings in an average stack
as a function
of density for different ion types, with a purely neutral system with
no ions for a reference. Four bold symbols in circles mark selected
systems shown in the snapshots in the bottom panel. (d) Fraction of
dangling rings, W(Ns =
1), i.e. rings not belonging to any cluster as a function of density.
(e) Snapshots of selected systems using the color code of Figure 1.
, of rings in an average stack
as a function
of density for different ion types, with a purely neutral system with
no ions for a reference. Four bold symbols in circles mark selected
systems shown in the snapshots in the bottom panel. (d) Fraction of
dangling rings, W(Ns =
1), i.e. rings not belonging to any cluster as a function of density.
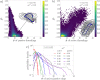
(e) Snapshots of selected systems using the color code of Figure 1.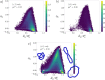
 and
and  .
.

References
-
- Micheletti C.; Marenduzzo D.; Orlandini E. Polymers with spatial or topological constraints: Theoretical and computational results. Phys. Rep. 2011, 504, 1–73. 10.1016/j.physrep.2011.03.003. - DOI
LinkOut - more resources
Full Text Sources

