Capturing dynamical correlations using implicit neural representations

Sathya R Chitturi^{1

2}, Zhurun Ji^{3

4}, Alexander N Petsch^{5

6

7}, Cheng Peng⁸, Zhantao Chen⁸, Rajan Plumley^{9

8

10}, Mike Dunne⁹, Sougata Mardanya¹¹, Sugata Chowdhury¹¹, Hongwei Chen¹², Arun Bansil¹², Adrian Feiguin¹², Alexander I Kolesnikov¹³, Dharmalingam Prabhakaran¹⁴, Stephen M Hayden¹⁵, Daniel Ratner⁹, Chunjing Jia^{9

8

16}, Youssef Nashed⁹, Joshua J Turner^{17

18}

Affiliations

¹ SLAC National Accelerator Laboratory, Menlo Park, CA, 94025, USA. chitturi@stanford.edu.
² Department of Materials Science and Engineering, Stanford University, Stanford, CA, 94305, USA. chitturi@stanford.edu.
³ Department of Physics and Applied Physics, Stanford University, Stanford, CA, 94305, USA. zhurun@stanford.edu.
⁴ Geballe Laboratory for Advanced Materials, Stanford University, Stanford, CA, 94305, USA. zhurun@stanford.edu.
⁵ SLAC National Accelerator Laboratory, Menlo Park, CA, 94025, USA. apetsch@stanford.edu.
⁶ Stanford Institute for Materials and Energy Sciences, Stanford University, Stanford, CA, 94305, USA. apetsch@stanford.edu.
⁷ H.H. Wills Physics Laboratory, University of Bristol, Bristol, BS8 1TL, UK. apetsch@stanford.edu.
⁸ Stanford Institute for Materials and Energy Sciences, Stanford University, Stanford, CA, 94305, USA.
⁹ SLAC National Accelerator Laboratory, Menlo Park, CA, 94025, USA.
¹⁰ Department of Physics, Carnegie Mellon University, Pittsburgh, PA, 15213, USA.
¹¹ Department of Physics and Astrophysics, Howard University, Washington, DC, USA.
¹² Department of Physics, Northeastern University, Boston, USA.
¹³ Neutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN, 37831, USA.
¹⁴ Department of Physics, University of Oxford, Clarendon Laboratory, Oxford, OX1 3PU, UK.
¹⁵ H.H. Wills Physics Laboratory, University of Bristol, Bristol, BS8 1TL, UK.
¹⁶ Department of Physics, University of Florida, Gainesville, FL, 32611, USA.
¹⁷ SLAC National Accelerator Laboratory, Menlo Park, CA, 94025, USA. joshuat@slac.stanford.edu.
¹⁸ Stanford Institute for Materials and Energy Sciences, Stanford University, Stanford, CA, 94305, USA. joshuat@slac.stanford.edu.

PMID: 37730824
PMCID: PMC10511537
DOI: 10.1038/s41467-023-41378-4

Capturing dynamical correlations using implicit neural representations

Sathya R Chitturi et al. Nat Commun. 2023.

. 2023 Sep 20;14(1):5852.

doi: 10.1038/s41467-023-41378-4.

Authors

Affiliations

¹ SLAC National Accelerator Laboratory, Menlo Park, CA, 94025, USA. chitturi@stanford.edu.
² Department of Materials Science and Engineering, Stanford University, Stanford, CA, 94305, USA. chitturi@stanford.edu.
³ Department of Physics and Applied Physics, Stanford University, Stanford, CA, 94305, USA. zhurun@stanford.edu.
⁴ Geballe Laboratory for Advanced Materials, Stanford University, Stanford, CA, 94305, USA. zhurun@stanford.edu.
⁵ SLAC National Accelerator Laboratory, Menlo Park, CA, 94025, USA. apetsch@stanford.edu.
⁶ Stanford Institute for Materials and Energy Sciences, Stanford University, Stanford, CA, 94305, USA. apetsch@stanford.edu.
⁷ H.H. Wills Physics Laboratory, University of Bristol, Bristol, BS8 1TL, UK. apetsch@stanford.edu.
⁸ Stanford Institute for Materials and Energy Sciences, Stanford University, Stanford, CA, 94305, USA.
⁹ SLAC National Accelerator Laboratory, Menlo Park, CA, 94025, USA.
¹⁰ Department of Physics, Carnegie Mellon University, Pittsburgh, PA, 15213, USA.
¹¹ Department of Physics and Astrophysics, Howard University, Washington, DC, USA.
¹² Department of Physics, Northeastern University, Boston, USA.
¹³ Neutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN, 37831, USA.
¹⁴ Department of Physics, University of Oxford, Clarendon Laboratory, Oxford, OX1 3PU, UK.
¹⁵ H.H. Wills Physics Laboratory, University of Bristol, Bristol, BS8 1TL, UK.
¹⁶ Department of Physics, University of Florida, Gainesville, FL, 32611, USA.
¹⁷ SLAC National Accelerator Laboratory, Menlo Park, CA, 94025, USA. joshuat@slac.stanford.edu.
¹⁸ Stanford Institute for Materials and Energy Sciences, Stanford University, Stanford, CA, 94305, USA. joshuat@slac.stanford.edu.

PMID: 37730824
PMCID: PMC10511537
DOI: 10.1038/s41467-023-41378-4

Abstract

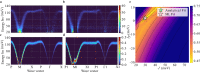
Understanding the nature and origin of collective excitations in materials is of fundamental importance for unraveling the underlying physics of a many-body system. Excitation spectra are usually obtained by measuring the dynamical structure factor, S(Q, ω), using inelastic neutron or x-ray scattering techniques and are analyzed by comparing the experimental results against calculated predictions. We introduce a data-driven analysis tool which leverages 'neural implicit representations' that are specifically tailored for handling spectrographic measurements and are able to efficiently obtain unknown parameters from experimental data via automatic differentiation. In this work, we employ linear spin wave theory simulations to train a machine learning platform, enabling precise exchange parameter extraction from inelastic neutron scattering data on the square-lattice spin-1 antiferromagnet La₂NiO₄, showcasing a viable pathway towards automatic refinement of advanced models for ordered magnetic systems.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interests.

Figures

**Fig. 1. Overview of machine learning pipeline, model Hamiltonian and reciprocal space paths.**
a Ni₄O₄ square-lattice plaquette in La₂NiO₄. J (J_p) is the first (second) nearest-neighbor interaction and a and b indicate the square-lattice unit vectors. b The Brillouin zone for the spin-1 square-lattice magnetic structure. Selected high-symmetry points are indicated. The two momentum paths are denoted by the purple and orange lines, respectively. c Visualization of the SIREN neural network for predicting the scalar dynamical structure factor intensity. All nodes in adjacent layers are connected to each other in a fully-connected architecture. The notation 64 × 3 and 64 × 1, represent three and one neural network layers with 64 neurons and with sinusoidal and linear activation functions, respectively. Neural network bias vectors are omitted for clarity. d Visualization of the distribution of training, test, and validation data in J-J_p space. e Synthetic S(Q, ω) predictions from the SIREN model along the corresponding trajectory shown in d. Grid lines correspond to [0, 50, 100, 150, 200] meV and [P, M, X, P, Γ, X] for the energy and wave vector, respectively.

**Fig. 2. Comparison between linear spin wave theory simulation and machine learning prediction for a given set of parameter values (J = 45.57 meV and J_p = 2.45 meV).**
a Example of ground-truth simulated S(Q, ω) calculated using the SpinW software program and b corresponding machine learning forward model prediction.

**Fig. 3. Hamiltonian parameter extraction via auto-differentiation of the neural implicit representation.**
a, b show experimental data after automated background subtraction. For the experimental data, the color bars reflect S(Q, ω) in units of: mbarnsr⁻¹meV⁻¹f.u.⁻¹. c, d show the corresponding machine learning predictions for the two paths. The predicted profiles are visually seen to be similar to the experimental data. Deviations at low ℏω are due to the neglect of anisotropic spin gaps in our model. e Visualization of the loss landscape for objective fitting in the Hamiltonian parameter space (J, J_p).

**Fig. 4. Real-time Hamiltonian parameter estimation using a differentiable implicit neural representation.**
a Machine learning prediction for J and J_p as a function of the total number of neutrons detected within the two path regions. Square-root scaling is used for the neutron counts due to the Poisson collection statistics. The machine learning prediction is seen to converge much earlier than the count-time recorded in the experiment. b Visualization of plausible low-count (without algorithmic background subtraction) data. Total number of neutrons detected with the two path regions are: 16,173, 57,237, and 326,952 (top to bottom). The colorbars show the absolute counts of detected neutrons.

See this image and copyright information in PMC

References

1. Chumak AV, Vasyuchka VI, Serga AA, Hillebrands B. Magnon spintronics. Nat. Phys. 2015;11:453–461. doi: 10.1038/nphys3347. - DOI
1. Neusser S, Grundler D. Magnonics: spin waves on the nanoscale. Adv. Mater. 2009;21:2927–2932. doi: 10.1002/adma.200900809. - DOI
1. Gutfleisch O, et al. Magnetic materials and devices for the 21st century: stronger, lighter, and more energy efficient. Adv. Mater. 2011;23:821–842. doi: 10.1002/adma.201002180. - DOI - PubMed
1. Rossat-Mignod J, et al. Neutron scattering study of the YBa2Cu3O6+x system. Phys. C: Supercond. 1991;185:86–92. doi: 10.1016/0921-4534(91)91955-4. - DOI
1. Chatterji, T. Neutron Scattering from Magnetic Materials (Elsevier, 2005).

Grants and funding

LinkOut - more resources

Full Text Sources

Save citation to file

Email citation

Add to Collections

Add to My Bibliography

Your saved search

Create a file for external citation management software

Your RSS Feed

Capturing dynamical correlations using implicit neural representations

Affiliations

Capturing dynamical correlations using implicit neural representations

Authors

Affiliations

Abstract

Conflict of interest statement

Figures

References

Grants and funding

LinkOut - more resources

Full Text Sources