Shoreline response to sea-level rise according to equilibrium beach profiles

Abstract

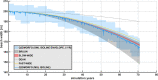
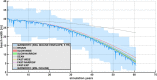
Shoreline position is a key parameter of a beach state, often used as a descriptor of the response of the system to changes in external forcing, such as sea-level rise. Changes in shoreline position are the result of coupled hydrodynamic and morphodynamic processes happening in the nearshore and acting at different temporal scales. Due to this complexity, methodologies aimed at reproducing shoreline evolution at decadal time scale require many simplifications. Simpler methods usually consider an equilibrium beach profile whose shape depends only on beach morphology, and whose location varies depending on incoming forcing. Here, we derive a general equation for shoreline evolution using equilibrium beach profiles. We particularize it based on several common assumptions, and evaluate changes on shoreline position caused by sea-level rise, combined with simultaneous wave and high-frequency sea-level forcing. We compare our model against other analytical equilibrium beach profile-based models and with a dynamic model explicitly computing sediment transport. Results indicate that: (i) it is necessary to consider the area of the emerged beach subject to marine forcing rather than focusing only on the submerged part, (ii) the rates of shoreline recession may change for narrow beaches, defined as those for which marine forcings act onto all of their aerial surface, and (iii) Bruun's Rule can describe beach shoreline evolution, but the uncertainty in selecting the landward boundary of the active profile entails a huge uncertainty in the magnitude of shoreline evolution. This problematic uncertainty can be drastically reduced if instantaneous forcing conditions are used instead of the arbitrary emerged/submerged active profile boundaries typically defined by only one statistic parameter of extreme conditions.

Figure 1

Proposed Fast EBP model for the wide beach case.

Figure 2

Predicted shoreline recession for an initial emerged beach width of 200 m (wide beach regime), under a parabolic sea-level rise (reaching 1 m at the end of the simulation period) with simultaneous high-frequency forcing. The average shoreline of Q2Dmorfo model and its dispersion are shown by a blue line and a blue shaded area, respectively. They are computed by interpolating the simulated topobathymetry to mean sea level and still-water level, respectively. The shoreline evolution from Ergodic Dean’s Rule is shown with a grey dotted line, that from Fast-Wide Rule is shown in yellow, and Bruun’s Rule is shown as a black shaded area (accounting for all possible emerged active profile boundary). Slow-Wide Rule is indicated by the red shaded area.

Figure 3

Predicted shoreline recession for an initial emerged beach width of 30 m (narrow beach regime), under a parabolic sea-level rise (reaching 1 m at the end of the simulation period), with simultaneous high-frequency forcing. Fast-Narrow Rule is indicated by the dashed magenta line, while Fast-Exponential Rule is indicated by the dashed white line. Also, Slow-Narrow Rule is depicted by the green shaded area. Refer to Fig. 2 for the meaning of the other lines and shaded areas. Note the Q2Dmorfo simulation ends before completing the 72 years study period, because the instantaneous shoreline (not the time-averaged shown in this figure) arrives to zero, thus ending the simulation.