Measuring prion propagation in single bacteria elucidates a mechanism of loss

Abstract

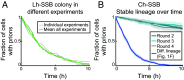
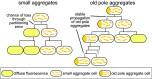
Prions are self-propagating protein aggregates formed by specific proteins that can adopt alternative folds. Prions were discovered as the cause of the fatal transmissible spongiform encephalopathies in mammals, but prions can also constitute nontoxic protein-based elements of inheritance in fungi and other species. Prion propagation has recently been shown to occur in bacteria for more than a hundred cell divisions, yet a fraction of cells in these lineages lost the prion through an unknown mechanism. Here, we investigate prion propagation in single bacterial cells as they divide using microfluidics and fluorescence microscopy. We show that the propagation occurs in two distinct modes. In a fraction of the population, cells had multiple small visible aggregates and lost the prion through random partitioning of aggregates to one of the two daughter cells at division. In the other subpopulation, cells had a stable large aggregate localized to the pole; upon division the mother cell retained this polar aggregate and a daughter cell was generated that contained small aggregates. Extending our findings to prion domains from two orthologous proteins, we observe similar propagation and loss properties. Our findings also provide support for the suggestion that bacterial prions can form more than one self-propagating state. We implement a stochastic version of the molecular model of prion propagation from yeast and mammals that recapitulates all the observed single-cell properties. This model highlights challenges for prion propagation that are unique to prokaryotes and illustrates the conservation of fundamental characteristics of prion propagation.

Keywords: Escherichia coli; microfluidics; prions; protein-based heredity; single-cell microscopy.

Fig. 1.

Experimental setup enables quantification of prion dynamics in single cells. (A) Transient expression of the S. cerevisiae New1 protein induces conversion of His6-mEYFP-Ch SSB PrD from its soluble form into the prion form in E. coli. Bacteria with prions have elevated levels of ClpB (due presumably to the upregulation of RpoH-dependent gene expression in cells containing threshold levels of aggregated protein); thus, bacterial colonies with prion-containing cells can be distinguished from colonies with cells containing the protein in the soluble form using a PclpB-lacZ transcriptional reporter [blue vs pale colonies, respectively, (31)]. (B) Blue colonies contain self-propagating aggregates. (Left) Replating blue colonies results in a mix of blue and pale colonies, while replating pale colonies results in only pale colonies. (Right) SDD-AGE shows that different blue colony cultures (A, B, and C) contain SDS-stable aggregates, whereas pale colony cultures contain only soluble Ch SSB PrD (prion formation was induced with New1-CFP; a gel where induction was done with New1-mScarlet-I can be found in SI Appendix, Fig. S1D). (C) Fluorescence microscopy images of E. coli expressing His6-mEYFP-Ch SSB PrD shows that cells from blue colonies display visible fluorescence aggregation, whereas cells from pale colonies display diffuse YFP fluorescence. (D) After prion conversion, cells from a blue colony are loaded in a microfluidic device where cells are trapped in dead-end trenches, and newborn cells are washed away by the flow of growth medium. Fluorescence time-lapse microscopy montage (kymographs) of individual lineages shows that cells propagate the aggregates for heterogeneous duration (I–III) before irreversibly reverting to diffuse fluorescence. YFP fluorescence is shown false-colored according to the colormap indicated on the graph. The prion loss called by our spot-finding algorithm is indicated by a yellow triangle. Cells that have diffuse fluorescence at the beginning of the experiments maintain it (IV). (E) The fraction of cells with prions over time (prion loss curve) for all aggregate phenotypes shows a biphasic decay, suggesting the presence of two distinct subpopulations ($n$ = 2,194 cells). (F) The prion loss curve for cells with small aggregates fits well to an exponential distribution (dashed line, R${}^2$ = 0.99, $n$ = 924 cells). Representative kymograph of cells with small aggregates (Top) (G) Loss curve for cells with old-pole aggregates ($n$ = 2,225 cells). Kymographs for the tracked cell (mother) and its progeny (Top). The old-pole aggregate is mostly immobile, and the progeny contain small aggregates. The colormap for the old-pole aggregate is different as these aggregates are brighter. The standard error on the mean (SEM) in E–G was estimated by bootstrapping, and an envelope is shown as 2$\times$ SEM ($N$ = 3 experiments for E–G).

Fig. 2.

Prion loss is driven by partitioning errors at cell division. (A) Schematic representation of the hypothesized mechanisms for prion loss in bacterial cells. (B) Median concentration of fluorescence (Ch SSB PrD) relative to the loss of the prion is constant ($n=$ 724 cells). The loss event is indicated with a dotted gray line at time 0. (C) Histogram of the cell cycle position at the time of loss, where 0 is defined as the moment immediately after a division and 1 immediately before. Most cells ($\sim$80%) lose the prion immediately after cell division ($n$ = 1,117 cells). (D) Kymographs of loss event show that prion loss happens in only one of the two daughter cells (86% of the losses, $n$ = 356 loss events). YFP fluorescence is shown false colored according to the colormap indicated on the graph. (E) Mean absolute partitioning errors at the cell divisions relative to prion loss ($n$ = 389 cells). The absolute partitioning error is constant prior to the loss, and higher than after the loss. (F) Mean partitioning errors in the cell divisions relative to the loss show that fluorescence is being transmitted to the daughter at the moment of loss for cells that lost the prion at the moment of cell division (blue lines). For the cells that lost the prion at a different moment of the cell cycle, this transfer happens one division prior to the loss (yellow line, $n$ = 389 cells total). For symmetric divisions, the average partitioning error would be $\sim$0, since molecules have an equal chance of being inherited by the mother or daughter cell. (G) Average longitudinal position of tracked aggregates shows that they move toward the daughter cell prior to the loss ($n$ = 1,117 cells; y axis indicates position along the length of the cell, averaged over all detected aggregates, with the negative values indicating the distance from the top of the trench at position 0. The envelopes represent 2$\times$ SEM in B and E–G ($N$ = 3 experiments).

Fig. 3.

Orthologous SSB cPrDs form self-propagating aggregates comparable to Ch SSB. (A) Prion loss curve for small aggregate cells of Lh SSB PrD ($n$ = 352 cells) and Ml SSB PrD ($n$ = 237 cells) compared to Ch SSB PrD from Fig. 1. Exponential fit curves are shown as dashed lines. (B) SDD-AGE of blue colonies confirms the presence of the aggregated prion form of Lh SSB and Ml SSB in cell extracts derived from blue colony cultures. Blue colonies with high, medium, and low prion content as estimated from fluorescence microscopy images were assayed (SI Appendix, Fig. S6E and section 3.1). (C) SSB orthologs form self-propagating aggregates for multiple generations. Replating blue colonies gives a mix of blue and pale colonies, while replating pale colonies results in exclusively pale colonies. (D) Fraction of prion losses at cell division shows that most losses happen at cell division for the different orthologs ($n$ = 1,117 cells for Ch, 394 cells for Lh, 282 cells for Ml). The error bars represent 2$\times$ SEM as estimated by bootstrapping. The expected fraction if loss is not correlated with cell division is shown as 1/number of time points per cell cycle, representing a uniform probability of loss at all points of the cell cycle. (E) Average longitudinal position (y) of tracked aggregates shows that they move toward the daughter cell prior to the loss for the different orthologs ($n=$ 396 cells for Lh, 282 cells for Ml). The envelopes represent 2$\times$ SEM in A and D and E ($N$ = 3 experiments).

Fig. 4.

Distinct bacterial lineages propagating identical prion protein exhibit distinct prion loss kinetics. (A) The experimental setup provides precise measurement of the prion loss kinetics. Prion loss curves for one colony of Lh SSB PrD in four different experiments (thin green lines, average in bold, $n=$ 815 cells total). (B) The prion loss curve for a stable lineage of Ch SSB PrD remains constant over multiple rounds of growth ($\sim$37 generations each, $n=$ 1,018 cells total). Round 1 refers to the first plating of induced cells cured of New1, and each subsequent round includes an overnight growth in liquid culture and plating on indicator medium. Round 2, 3, and 4 cells were obtained from a colony culture inoculated from Round 2, 3, and 4 colonies, respectively. Another lineage (from Fig. 1, dark blue line) is shown as a comparison. The envelopes represent 2$\times$ SEM as estimated by bootstrapping.

Fig. 5.

A stochastic nucleated polymerization model recapitulates the experimental results. (A) A stochastic model of prion propagation in growing and dividing cells. Soluble fold protein numbers, denoted by X, are produced at a rate that scales with the cell volume. This phenomenological rate ensures that the concentration of soluble fold proteins is produced constitutively and reaches a cell-cycle independent state, in effect recapitulating the homeostasis of protein concentrations in exponentially growing cells (46) (SI Appendix, sections 3.2.1 and 3.2.8). The number of prion fold aggregates made of $k$ proteins is denoted by $Y_k$, where $k=1,2,3,\cdots$. When a soluble fold protein collides with an aggregate of size $k$, it is converted with fixed probability to prion fold by elongating the aggregate to size $k+1$. Assuming an equal distribution of aggregates in the cell volume, it follows (47) that the soluble fold proteins are converted to prion fold with a reaction rate proportional to the protein concentrations. Similarly, chaperone-mediated fragmentation follows a reaction that is proportional to the aggregate concentrations, with each binding between any two monomers having the same probability of splitting. Concentrations are given by dividing the protein numbers by the cell volume, which grows exponentially from $V_0$ to $2V_0$ between divisions with a fixed doubling time. At cell division, protein numbers are split randomly, with each soluble protein and each aggregate having a 50% chance of remaining in the cell. (B) Soluble fold production parameter $\lambda V_0$ was estimated to be $1.75$ min${}^{-1}$ by comparing the measured partitioning error of cells after loss of prions with their respective simulations (SI Appendix, section 3.2.3.2). With no minimal seed size $n_c=0$ (see SI Appendix, section 3.2.5 for $n_c=2$), a parameter sweep of elongation and fragmentation parameters shows that prions in cells with larger fragmentation and elongation rates are more stable. An average time of loss of 129.26 min was measured in the experiment shown in Fig. 1F, with the corresponding contour indicated by the dashed orange line. (C) Cells with smaller fragmentation rates and larger elongation rates have larger partitioning errors prior to loss. An absolute partitioning error prior to loss of 0.125 was measured in the experiment shown in Fig. 2E, with the corresponding contour indicated by the dashed orange line. Using the two contour plots from B and C, we find the model parameters that match the measured time of loss and partitioning error, indicated by the orange dot. (D) Time of loss curves follow an exponential, in agreement with Fig. 1F. Plotted are the time of loss curves for systems with parameters along the solid orange line in B. Loss is defined as when $Y_k=0$ for all $k$. (E) The model can predict the aggregate size distribution prior to loss, showing that smaller aggregates are more stable in this parameter regime. (F) The total protein concentration is approximately constant leading up to the loss, in agreement with Fig. 2B. (G) In this model the prion state is always lost at cell division. (H) Absolute partitioning errors are larger before the loss, in agreement with Fig. 2E. (I) A large negative partitioning error occurs at the time of loss, in agreement with Fig. 2F.

Fig. 6.

Schematic of the two observed modes of prion propagation. Cells with small aggregates have a probability of losing the prion at each cell division through partitioning errors. At cell division, an old-pole aggregate cell generates a small aggregate cell and an old-pole aggregate cell. Although the old-pole aggregate is very stable, the cells containing old-pole aggregates represent a small fraction of a growing culture. The small aggregate cells generated through this division presumably propagate the prion similarly to the other observed small aggregate cells.