A Novel Quantitative Metric Based on a Complete and Unique Characterization of Neural Network Activity: 4D Shannon's Entropy

Abstract

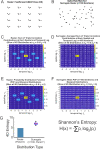
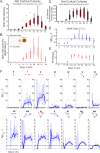
The human brain comprises an intricate web of connections that generate complex neural networks capable of storing and processing information. This information depends on multiple factors, including underlying network structure, connectivity, and interactions; and thus, methods to characterize neural networks typically aim to unravel and interpret a combination of these factors. Here, we present four-dimensional (4D) Shannon's entropy, a novel quantitative metric of network activity based on the Triple Correlation Uniqueness (TCU) theorem. Triple correlation, which provides a complete and unique characterization of the network, relates three nodes separated by up to four spatiotemporal lags. Here, we evaluate the 4D entropy from the spatiotemporal lag probability distribution function (PDF) of the network activity's triple correlation. Given a spike raster, we compute triple correlation by iterating over time and space. Summing the contributions to the triple correlation over each of the spatial and temporal lag combinations generates a unique 4D spatiotemporal lag distribution, from which we estimate a PDF and compute Shannon's entropy. To outline our approach, we first compute 4D Shannon's entropy from feedforward motif-class patterns in a simulated spike raster. We then apply this methodology to spiking activity recorded from rat cortical cultures to compare our results to previously published results of pairwise (2D) correlated spectral entropy over time. We find that while first- and second-order metrics of activity (spike rate and cross-correlation) show agreement with previously published results, our 4D entropy computation (which also includes third-order interactions) reveals a greater depth of underlying network organization compared to published pairwise entropy. Ultimately, because our approach is based on the TCU, we propose that 4D Shannon's entropy is a more complete tool for neural network characterization.

Fig. 1. [22]: Triple correlation relates three nodes separated by up to two spatial and two temporal lags.

(A) Given a spike raster, (B) autocorrelation (AC) relates two nodes separated by one temporal lag, cross-correlation (CC) relates two nodes separated by one spatial and one temporal lag, and triple correlation (TC) relates three nodes separated by up to two spatial and two temporal lags. These three-node configurations can be collapsed into (C) fourteen motif classes (0-XIII) which can embody well-studied neuronal processing properties. The fourteen motif classes are termed the motif-class spectrum. Figure reprinted with permission from authors and under the terms of the Creative Commons CC BY license from [22].

Fig. 2:. Overview of method to compute probability distribution function (PDF) and associated 4D entropy from the triple correlation of a simulated spike raster.

(A) Given a spike raster of isolated feedforward motif class patterns and (B) one instance of a spike-rate matched surrogate (shuffled) raster (n=100 iterations), we compute triple correlation (using temporal lags from −4:4 bins and spatial lags from −5:5 bins for this example) and (C-D) sum the contributions to the triple correlation at each spatial and temporal lag combination for the feedforward network raster and the surrogate raster (average distribution for 100 iterations). (E-F) From this, we estimate the PDF. (G) 4D Shannon’s entropy computed for the raster and the whisker plot for the 100 surrogates.

Figure 3:. Characterizing network activity of rat cortical cultures over time using 4D entropy and the motif-class spectrum.

(A) The spike rate from the published data (B) and triple correlation (motif class 0) show similar trends from 2–35 days in vitro (DIV). (C) The 2D correlated spectral entropy (CorSE) from the published data as well as (D) the prevalence of motif class V (pairwise 2D spike propagation) also show comparable trends. (E) The 4D entropy computation based on triple correlation shows a comparable trend from 2–17 DIV but does not decrease from 21–35 DIV, even though the spike rate (A-B) and second-order pairwise metrics (C-D) show this decrease from 31–35 DIV. (F) The fourteen motif-class profiles from triple correlation provide insight into individual network patterns. Motif classes V (cross-correlation; same as Panel D) and XIII (feedforward spike propagation) show similar trends to that of the published 2D CorSE values in that they gradually increase, peak around 24–28 DIV, and then decrease to network activity comparable to chance. Motif classes II, XI-XII also peak around 24–28 and decrease from 31–35 DIV, but do not revert to activity comparable to chance from 31–35. Boxes in the box-and-whisker plots represent the 25^th, 50^th (median), and 75^th percentiles, and the whiskers indicate the range of the data.