The Best Models of Bodipy's Electronic Excited State: Comparing Predictions from Various DFT Functionals with Measurements from Femtosecond Stimulated Raman Spectroscopy

Abstract

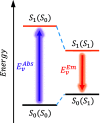
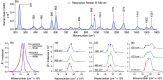
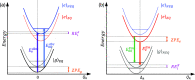
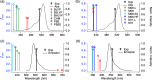
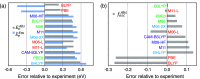
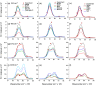
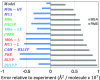
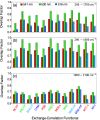
Density functional theory (DFT) and time-dependent DFT (TD-DFT) are pivotal approaches for modeling electronically excited states of molecules. However, choosing a DFT exchange-correlation functional (XCF) among the myriad of alternatives is an overwhelming task that can affect the interpretation of results and lead to erroneous conclusions. The performance of these XCFs to describe the excited-state properties is often addressed by comparing them with high-level wave function methods or experimentally available vertical excitation energies; however, this is a limited analysis that relies on evaluation of a single point in the excited-state potential energy surface (PES). Different strategies have been proposed but are limited by the difficulty of experimentally accessing the electronic excited-state properties. In this work, we have tested the performance of 12 different XCFs and TD-DFT to describe the excited-state potential energy surface of Bodipy (2,6-diethyl-1,3,5,7-tetramethyl-8-phenyldipyrromethene difluoroborate). We compare those results with resonance Raman spectra collected by using femtosecond stimulated Raman spectroscopy (FSRS). By simultaneously fitting the absorption spectrum, fluorescence spectrum, and all of the resonance Raman excitation profiles within the independent mode displaced harmonic oscillator (IMDHO) formalism, we can describe the PES at the Franck-Condon (FC) region and determine the solvent and intramolecular reorganization energy after relaxation. This allows a direct comparison of the TD-DFT output with experimental observables. Our analysis reveals that using vertical absorption energies might not be a good criterion to determine the best XCF for a given molecular system and that FSRS opens up a new way to benchmark the excited-state performance of XCFs of fluorescent dyes.

Figure 1

Bodipy: 2,6-Diethyl-1,3,5,7-tetramethyl-8-phenyldipyrromethene difluoroborate.

Figure 2

Calculation of the vertical absorption (E_v^Abs) and emission (E_v^Em) energies using DFT/TD-DFT and the SS-PCM formalism. Absorption is initiated from the ground electronic state at the equilibrium geometry and solvent polarization of the ground state, S₀(S₀), and places the molecule in the excited electronic state but with the nuclear geometry and solvent polarization of the ground state, S₁(S₀). Emission is initiated at the excited-state equilibrium geometry and solvent polarization of the excited state, S₁(S₁), and places the molecule in the ground state but with the nuclear and solvent polarization of the excited state, S₀(S₁).

Figure 3

(a) 530 nm Raman pump FSRS spectrum (blue) and fit used to compute the Raman cross section (gray). The asterisk marks a residual feature from solvent subtraction. (b) Experimental absorption and emission spectra and the calculated absolute cross sections. Experimental and calculated resonance Raman cross section of the most intense vibrational modes in the (c) low-, (d) mid-, and (e) high-frequency region at each Raman pump wavelength. The calculated Raman cross sections are presented as solid lines.

Figure 4

Ground (|g⟩) and excited (|e⟩) potential energy surfaces within the IMDHO model. The |e⟩ is presented at two different solvent regimes: equilibrium (eq), in red, and nonequilibrium (neq), in blue. Transitions energies benchmarked in this work: the vertical absorption energy, E_v^Abs (purple), and the vertical emission energy, E_v^Em (green), are obtained directly from TD-DFT. ZPE_g and ZPE_e are the zero-point vibrational energies for the ground and excited state, respectively. Similarly, RE_g^int and RE_e^int are the intramolecular reorganization energy for the ground and excited state. E₀₀^Abs and E₀₀^Em are experimentally measurable “0–0” energy for absorption and emission. Note that within the IMDHO model, the zero-point vibrational energy and the intramolecular reorganization energy are the same for both the |g⟩ and |e⟩ electronic states.

Figure 5

Experimental (black) and TD-DFT-calculated oscillator strengths (f_osc^Abs) plotted against the vertical absorption energies (E_v^Abs) for each (a) GGA and (b) mGGA XCF. TD-DFT-calculated vertical emission energies (E_v^Em) for each (c) GGA and (d) mGGA XCF. The experimental absorption (a,b) and emission (c,d) spectra are included. For parts (c) and (d), we use the same f_osc^Abs as in parts (a) and (b), obtained from integrating the absorption spectra. Here “CAM” corresponds to CAM-B3LYP. Vertical energies were computed at the SS-PCM/TD-DFT level, and S₁ geometry optimization was performed at the LR-PCM/TD-DFT level with benzene as the PCM solvent.

Figure 6

Differences between the DFT-calculated (a) E_v^Abs, E_v^Em, and (b) f_osc^Abs with the experiment.

Figure 7

(a) Each bar shows the RE_T^DFT for every XCF, where the upper bar is S₁(S₀) and the lower bar is given by S₁(S₁). The experimental RE_T (black) is given by E_v^Abs and (E_v^Abs – RE_T). (b) The error is calculated as (RE_T^DFT – RE_T). Vertical energies were computed at the SS-PCM/TD-DFT level, and S₁ geometry optimization was performed at the LR-PCM/TD-DFT level, with benzene as the PCM solvent.

Figure 8

Comparison between the TD-DFT/DFT-calculated, experimental (points), and modeled (black dashed) RR excitation profile for four vibrational modes: 241 (a–c), 602 (d–f), 1172 (g–i), and 1410 (j–l) cm^–1. On top of the experimental and modeled profiles are the DFT profiles calculated using the labeled functionals.

Figure 9

RMS and MSA difference (in Ų/molecule) between the experimental and calculated RREP. “Model” is the IMDHO fitting to the experimental data; DFT results are ranked from the best to worst.

Figure 10

Experimental (black) and DFT-calculated RR spectra using (a) GGA and (b) mGGA XCFs. The excitation wavelength is 530 nm. All of the RR spectra are normalized relative to the most intense peak.

Figure 11

(a) Overlap factor obtained at three different excitation wavelengths: 541 (red), 530 (green), and 516 (blue) nm. The overlap factor was also calculated for the (b) low-frequency (200–1000 cm^–1) and (c) high-frequency (1000–1700 cm^–1) regions of the RR spectrum. Here, “CAM” corresponds to CAM-B3LYP.