Studying stochastic systems biology of the cell with single-cell genomics data
- PMID: 37751736
- PMCID: PMC10725240
- DOI: 10.1016/j.cels.2023.08.004
Studying stochastic systems biology of the cell with single-cell genomics data
Abstract
Recent experimental developments in genome-wide RNA quantification hold considerable promise for systems biology. However, rigorously probing the biology of living cells requires a unified mathematical framework that accounts for single-molecule biological stochasticity in the context of technical variation associated with genomics assays. We review models for a variety of RNA transcription processes, as well as the encapsulation and library construction steps of microfluidics-based single-cell RNA sequencing, and present a framework to integrate these phenomena by the manipulation of generating functions. Finally, we use simulated scenarios and biological data to illustrate the implications and applications of the approach.
Keywords: Fokker-Planck equations; Markov chains; bioinformatics; chemical master equations; genomics; single-cell RNA sequencing; single-cell genomics; single-cell transcriptomics; stochastic differential equations; stochastic processes; transcriptomics.
Copyright © 2023 Elsevier Inc. All rights reserved.
Conflict of interest statement
Declaration of interests The authors declare no competing interests.
Figures
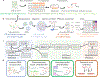
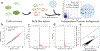

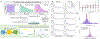
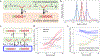
Update of
-
Studying stochastic systems biology of the cell with single-cell genomics data.bioRxiv [Preprint]. 2023 May 29:2023.05.17.541250. doi: 10.1101/2023.05.17.541250. bioRxiv. 2023. Update in: Cell Syst. 2023 Oct 18;14(10):822-843.e22. doi: 10.1016/j.cels.2023.08.004. PMID: 37292934 Free PMC article. Updated. Preprint.
Similar articles
-
Studying stochastic systems biology of the cell with single-cell genomics data.bioRxiv [Preprint]. 2023 May 29:2023.05.17.541250. doi: 10.1101/2023.05.17.541250. bioRxiv. 2023. Update in: Cell Syst. 2023 Oct 18;14(10):822-843.e22. doi: 10.1016/j.cels.2023.08.004. PMID: 37292934 Free PMC article. Updated. Preprint.
-
Multivariate Markov processes for stochastic systems with delays: application to the stochastic Gompertz model with delay.Phys Rev E Stat Nonlin Soft Matter Phys. 2002 Jul;66(1 Pt 1):011914. doi: 10.1103/PhysRevE.66.011914. Epub 2002 Jul 26. Phys Rev E Stat Nonlin Soft Matter Phys. 2002. PMID: 12241391
-
Stochastic approaches in systems biology.Wiley Interdiscip Rev Syst Biol Med. 2010 Jul-Aug;2(4):385-397. doi: 10.1002/wsbm.78. Wiley Interdiscip Rev Syst Biol Med. 2010. PMID: 20836037 Review.
-
Multiscale Stochastic Reaction-Diffusion Algorithms Combining Markov Chain Models with Stochastic Partial Differential Equations.Bull Math Biol. 2019 Aug;81(8):3185-3213. doi: 10.1007/s11538-019-00613-0. Epub 2019 Jun 4. Bull Math Biol. 2019. PMID: 31165406 Free PMC article.
-
A comparison of deterministic and stochastic approaches for sensitivity analysis in computational systems biology.Brief Bioinform. 2020 Mar 23;21(2):527-540. doi: 10.1093/bib/bbz014. Brief Bioinform. 2020. PMID: 30753281 Review.
Cited by
-
Quantifying and correcting bias in transcriptional parameter inference from single-cell data.Biophys J. 2024 Jan 2;123(1):4-30. doi: 10.1016/j.bpj.2023.10.021. Epub 2023 Oct 27. Biophys J. 2024. PMID: 37885177 Free PMC article.
-
kallisto, bustools, and kb-python for quantifying bulk, single-cell, and single-nucleus RNA-seq.bioRxiv [Preprint]. 2024 Jan 23:2023.11.21.568164. doi: 10.1101/2023.11.21.568164. bioRxiv. 2024. Update in: Nat Protoc. 2025 Mar;20(3):587-607. doi: 10.1038/s41596-024-01057-0. PMID: 38045414 Free PMC article. Updated. Preprint.
-
Solving stochastic gene-expression models using queueing theory: A tutorial review.Biophys J. 2024 May 7;123(9):1034-1057. doi: 10.1016/j.bpj.2024.04.004. Epub 2024 Apr 9. Biophys J. 2024. PMID: 38594901 Free PMC article. Review.
-
Fokker-Planck diffusion maps of microglial transcriptomes reveal radial differentiation into substates associated with Alzheimer's pathology.Commun Biol. 2025 Feb 22;8(1):279. doi: 10.1038/s42003-025-07594-y. Commun Biol. 2025. PMID: 39987247 Free PMC article.
-
Incorporating spatial diffusion into models of bursty stochastic transcription.J R Soc Interface. 2025 Apr;22(225):20240739. doi: 10.1098/rsif.2024.0739. Epub 2025 Apr 9. J R Soc Interface. 2025. PMID: 40199347 Free PMC article.
References
-
- Wilkinson DJ, 2018. Stochastic modelling for systems biology. Chapman and Hall/CRC.
-
- Waddington CH, 1957. The strategy of the genes. Routledge.
-
- Huang S, 2009. Reprogramming cell fates: reconciling rarity with robustness. BioEssays 31:546–560. https://onlinelibrary.wiley.com/doi/abs/10.1002/bies.200800189. - DOI - PubMed
-
- Huang S, 2012. The molecular and mathematical basis of Waddington’s epigenetic landscape: A framework for post-Darwinian biology? BioEssays 34:149–157. https://onlinelibrary.wiley.com/doi/abs/10.1002/bies.201100031. - DOI - PubMed
-
- Rand DA, Raju A, Sáez M, Corson F, and Siggia ED, 2021. Geometry of gene regulatory dynamics. Proceedings of the National Academy of Sciences 118:e2109729118. https://pnas.org/doi/full/10.1073/pnas.2109729118. - DOI - PMC - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources

