Group-level brain decoding with deep learning

Abstract

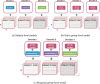
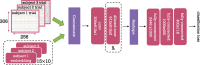
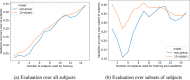
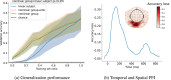
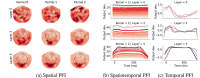
Decoding brain imaging data are gaining popularity, with applications in brain-computer interfaces and the study of neural representations. Decoding is typically subject-specific and does not generalise well over subjects, due to high amounts of between subject variability. Techniques that overcome this will not only provide richer neuroscientific insights but also make it possible for group-level models to outperform subject-specific models. Here, we propose a method that uses subject embedding, analogous to word embedding in natural language processing, to learn and exploit the structure in between-subject variability as part of a decoding model, our adaptation of the WaveNet architecture for classification. We apply this to magnetoencephalography data, where 15 subjects viewed 118 different images, with 30 examples per image; to classify images using the entire 1 s window following image presentation. We show that the combination of deep learning and subject embedding is crucial to closing the performance gap between subject- and group-level decoding models. Importantly, group models outperform subject models on low-accuracy subjects (although slightly impair high-accuracy subjects) and can be helpful for initialising subject models. While we have not generally found group-level models to perform better than subject-level models, the performance of group modelling is expected to be even higher with bigger datasets. In order to provide physiological interpretation at the group level, we make use of permutation feature importance. This provides insights into the spatiotemporal and spectral information encoded in the models. All code is available on GitHub (https://github.com/ricsinaruto/MEG-group-decode).

Keywords: MEG; decoding; deep learning; neuroimaging; permutation feature importance; transfer learning.

FIGURE 1

Comparison of subject‐level (a), naive group‐level (b), the proposed group‐level (c) modelling. (a) A separate model is trained on the trials (examples) of each subject. (b) A single, shared model is trained on the trials of all subjects without capturing between‐subject variability. (c) A single, shared model is trained on the trials of all subjects with an additional embedding component that is subject‐specific. Each trial is C × T (channels × time points) dimensional. Each of the s subjects has t trials.

FIGURE 2

Group‐level WaveNet Classifier with subject embeddings. Dashed boxes represent parts of the model which differ between subject‐level and group‐level versions of our architecture. Red boxes represent learnable parameters. For convolutional layers, the numbers represent input channels × output channels × kernel size. For fully‐connected layers, the numbers represent input neurons × output neurons. The embedding layer dimensionality is given as s × E (15 × 10), where s is number of subjects, and E is the embedding size. Embeddings are concatenated with input trials to provide information about which trial is coming from which subject. The classification loss is cross‐entropy.

FIGURE 3

Trained subject‐level and group‐level models evaluated on the validation set of each subject. Wilcoxon signed‐rank tests are shown for comparisons of interest (${}^{*}=p<5e-2,{}^{*}*=p<1e-2,{}^{*}**=p<1e-3,{}^{*}***=p<1e-4$). The non‐linear group‐emb finetuned model is finetuned separately on each subject, initialized with the non‐linear group‐emb model. Chance level is 1/118.

FIGURE 4

Accuracy changes across all 15 subjects (individual colours), when comparing trained linear subject, non‐linear group‐emb and non‐linear group‐emb finetuned models. Both non‐linear group‐emb and the finetuned version clearly reduce the variability of accuracies across subjects and are especially helpful for low‐accuracy subjects. When finetuning non‐linear group‐emb on individual subjects (c), we can see that accuracy increases for all subjects, and especially for high‐accuracy subjects. This is unsurprising because these subjects have good enough data on their own for subject‐level models to be able to learn well. As seen in (a) and (b) these high‐accuracy subjects are usually impaired by group‐level models, exactly for the aforementioned reason.

FIGURE 5

(a) Validation accuracy over all subjects with respect to increasing the subset of subjects used for training the sub‐group model (blue line) on the horizontal axis. The 15‐subject model (orange line) is our standard non‐linear group‐emb model trained on all subjects. (b) Validation accuracy over the subset of subjects used for training the sub‐group model (blue line). The 15‐subject model (orange line) is our standard non‐linear group‐emb model trained on all subjects. The 15‐subject model is evaluated on the same increasing sets of subjects as used for the sub‐group models.

FIGURE 6

(a) Generalisation and finetuning on left‐out subjects. The horizontal axis shows the amount of training data used from the left‐out subject; a training set ratio of 0 corresponds to a zero‐shot approach. Linear subject is trained from scratch, while non‐linear group‐emb and non‐linear group are initialised with the trained non‐linear group‐level model with and without embeddings, respectively. The 95% confidence interval of the accuracy across left‐out subjects is shown with shading. (b) Temporal (line) and spatial (sensor space map) PFI for the trained non‐linear group‐emb model. For temporal PFI accuracy loss (vertical axis) is plotted with respect to time since visual image presentation (horizontal axis). Shading shows the 95% confidence interval which is not visible due to low variability. For spatial PFI, darker red shading is equivalent to higher accuracy loss.

FIGURE 7

Spatio‐temporal insights can be obtained using PFI. Spatial (a), channel‐wise temporal (b) and temporal (c) PFI across non‐linear group‐emb kernels within 3 layers (rows). For spatial PFI, kernels are plotted separately; whereas for temporal PFI, 5 kernels (lines) are plotted together. Channel‐wise temporal PFI shows the temporal PFI of each channel for Kernel 2. Channel colouring is matched to the corresponding spatial PFI map, and darker reds mean higher output deviation. For temporal PFI, output deviation is normalised. The horizontal axis shows the time elapsed since the image presentation, for both temporal PFI types. 95% confidence intervals are shown with shading.

FIGURE 8

Frequency sensitivity of kernels via spectral PFI (a), channel‐wise spectral PFI (b), and frequency characteristics via kernel FIR analysis (c), from 3 layers (rows). Kernels are plotted together (lines) for spectral PFI, and in separate columns for kernel FIR analysis (normalised). Each channel‐wise spectral PFI plot is for 1 kernel, where lines show the spectral PFI of corresponding channels in the sensor space map. 95% confidence intervals are shown with shading for spectral PFI. Due to small variability across permutations, this is barely visible. For spectral PFI the band‐width was set to 5 Hz to obtain a smooth frequency profile.