Estimating seroconversion rates accounting for repeated infections by approximate Bayesian computation
- PMID: 37753713
- PMCID: PMC10842067
- DOI: 10.1002/sim.9906
Estimating seroconversion rates accounting for repeated infections by approximate Bayesian computation
Abstract
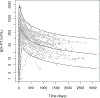
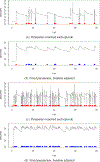
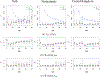
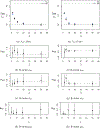
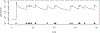
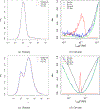
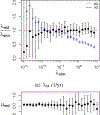
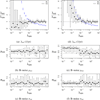
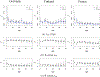
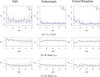
This study presents a novel approach for inferring the incidence of infections by employing a quantitative model of the serum antibody response. Current methodologies often overlook the cumulative effect of an individual's infection history, making it challenging to obtain a marginal distribution for antibody concentrations. Our proposed approach leverages approximate Bayesian computation to simulate cross-sectional antibody responses and compare these to observed data, factoring in the impact of repeated infections. We then assess the empirical distribution functions of the simulated and observed antibody data utilizing Kolmogorov deviance, thereby incorporating a goodness-of-fit check. This new method not only matches the computational efficiency of preceding likelihood-based analyses but also facilitates the joint estimation of antibody noise parameters. The results affirm that the predictions generated by our within-host model closely align with the observed distributions from cross-sectional samples of a well-characterized population. Our findings mirror those of likelihood-based methodologies in scenarios of low infection pressure, such as the transmission of pertussis in Europe. However, our simulations reveal that in settings of higher infection pressure, likelihood-based approaches tend to underestimate the force of infection. Thus, our novel methodology presents significant advancements in estimating infection incidence, thereby enhancing our understanding of disease dynamics in the field of epidemiology.
Keywords: approximate Bayesian computation; empirical distribution function; reinfection; seroincidence.
© 2023 John Wiley & Sons Ltd.
Figures
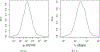



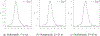

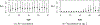


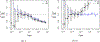

References
-
- de Greeff SC, Teunis P, de Melker HE, et al. Two-component cluster analysis of a large serodiagnostic database for specificity of increases of IgG antibodies against pertussis toxin in paired serum samples and of absolute values in single serum samples. Clinical and Vaccine Immunology 2012;19(9):1452–1456. doi:10.1128/CVI.00229-12. - DOI - PMC - PubMed
-
- Konda T, Kamachi K, Iwaki M, Matsunaga Y. Distribution of pertussis antibodies among different age groups in Japan. Vaccine 2002;20:1711–1717. - PubMed
-
- Peasey AE, Ruiz-Palacios GM, Quigley M, et al. Seroepidemiology and risk factors for sporadic norovirus/Mexico strain. Journal of Infectious Diseases 2004;189(11):2027–2036. - PubMed
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
