Spearman-like correlation measure adjusting for covariates in bivariate survival data
- PMID: 37753794
- PMCID: PMC10897866
- DOI: 10.1002/bimj.202200137
Spearman-like correlation measure adjusting for covariates in bivariate survival data
Abstract
We propose an extension of Spearman's correlation for censored continuous and discrete data that permits covariate adjustment. Previously proposed nonparametric and semiparametric Spearman's correlation estimators require either nonparametric estimation of the bivariate survival surface or parametric assumptions about the dependence structure. In practice, nonparametric estimation of the bivariate survival surface is difficult, and parametric assumptions about the correlation structure may not be satisfied. Therefore, we propose a method that requires neither and uses only the marginal survival distributions. Our method estimates the correlation of probability-scale residuals, which has been shown to equal Spearman's correlation when there is no censoring. Because this method relies only on marginal distributions, it tends to be less variable than the previously suggested nonparametric estimators, and the confidence intervals are easily constructed. Although under censoring, it is biased for Spearman's correlation as our simulations show, it performs well under moderate censoring, with a smaller mean squared error than nonparametric approaches. We also extend it to partial (adjusted), conditional, and partial-conditional correlation, which makes it particularly relevant for practical applications. We apply our method to estimate the correlation between time to viral failure and time to regimen change in a multisite cohort of persons living with HIV in Latin America.
Keywords: Spearman's correlation; bivariate survival data; nonparametric; probability-scale residuals; semiparametric.
© 2023 Wiley-VCH GmbH.
Conflict of interest statement
Conflict of Interest
The authors have declared no conflict of interest.
Figures
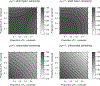

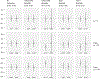

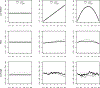
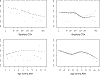
References
-
- Belzile L. and Genest C. (2017). lcopula: Liouville Copulas. [R package version 1.0. https://CRAN.R-project.org/package=lcopula (accessed January 3, 2022)]
-
- Breslow NE (1972). Discussion of Professor Cox’s paper. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 34, 216–217.
-
- Carriere JF (2000). Bivariate survival models for coupled lives. Scandinavian Actuarial Journal 2000, 17–32.
-
- CCASAnet (2020). Times to viral failure and regimen change data. [Anonymized for presentation, https://biostat.app.vumc.org/ArchivedAnalyses/ (accessed January 3, 2022)]
-
- Cesar C. and Jenkins CA and Shepherd BE and Padgett D. and Mejía F. and Ribeiro SR and Cortes CP and Pape JW and Madero JS and Fink V. and others (2015). Incidence of virological failure and major regimen change of initial combination antiretroviral therapy in the Latin America and the Caribbean: an observational cohort study. The Lancet HIV 2, e492–e500. - PMC - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

