Rheology of Gels and Yielding Liquids

Abstract

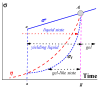
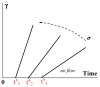
In this review, today's state of the art in the rheology of gels and transition through the yield stress of yielding liquids is discussed. Gels are understood as soft viscoelastic multicomponent solids that are in the incomplete phase separation state, which, under the action of external mechanical forces, do not transit into a fluid state but rupture like any solid material. Gels can "melt" (again, like any solids) due to a change in temperature or variation in the environment. In contrast to this type of rheology, yielding liquids (sometimes not rigorously referred to as "gels", especially in relation to colloids) can exist in a solid-like (gel-like) state and become fluid above some defined stress and time conditions (yield stress). At low stresses, their behavior is quite similar to that of permanent solid gels, including the frequency-independent storage modulus. The gel-to-sol transition considered in colloid chemistry is treated as a case of yielding. However, in many cases, the yield stress cannot be assumed to be a physical parameter since the solid-to-liquid transition happens in time and is associated with thixotropic effects. In this review, special attention is paid to various time effects. It is also stressed that plasticity is not equivalent to flow since (irreversible) plastic deformations are determined by stress but do not continue over time. We also discuss some typical errors, difficulties, and wrong interpretations of experimental data in studies of yielding liquids.

Keywords: flow; gel; gel-like state; yield stress; yielding liquids.

Figure 1

A rheological model of gelation.

Figure 2

Possible modes of break-up–elastic (a), viscoelastic (b), and delayed (c). The last point on all curves corresponds to the time of fracture (marked by a red point).

Figure 3

Evolution of the storage modulus in the process of gelation (scheme).

Figure 4

Viscoelastic properties of wormlike micelles (from [57] with permission).

Figure 5

Flow curves–dependences of the apparent viscosity on shear stress (a) and frequency dependences of the storage modulus (b) in the gel-like state of low stresses for concentrated emulsions (these objects are liquid explosives.

Figure 6

Viscoelastic properties of the aqueous solutions of poly(ethylene oxide) with different concentrations (shown in the curves) in the presence of 3 vol.% of SiO_2. Filled symbols–storage modulus G′; open symbols–loss modulus, G″.

Figure 7

Experimental data for highly concentrated emulsions for the gel-like region (a) and “complete” flow curves (b). As an emulsion stabilizer, a mixture of gelatin (C_G = 0.5 wt.%) with κ-carrageenan (C_car, wt.%—shown in the figures) is used.

Figure 8

A general diagram illustrating the dependence of any false upper Newtonian limit on the time effect. The presented data were obtained for highly concentrated emulsions.

Figure 9

Concentration dependence of the yield stress for dispersions of carbon black (surface 300 m²/g) in different matrix–poly(butadiene)s with M_w = 1.35 × 10⁵ and 1 × 10⁴ Da and low-viscosity silicon oil–marked with various symbols; with various symbols calculated by the Casson and the Herschel–Bulkley models [106], and by G′ (σ₀) curves. Original data.

Figure 10

Determination of the yield stress by the Herschel–Bulkley model and the Casson model for hydrogel of gelatin-κ-carrageenan complexes (C_g = 1.0 wt.%). The change in the κ-carrageenan concentration is indicated by arrows, C_car, wt.%: 6–0.100, 7–0.150, 8–0.175, 9–0.200, 10–0.400, 11–0.500.

Figure 11

Various methods and results of extrapolation (number of lower curves) of experimental data–points and the fitting curve.

Figure 12

Stress up-and-down scanning in measuring the flow curve. Curves 1, 2, and 3 correspond to a decreasing rate of scanning in decreasing shear stress (along the blue arrow).

Figure 13

Developing deformation γ on time–Bingham yielding. The dotted arrows show the increase in shear stress.

Figure 14

Development of deformations in transition from the gel-like to plastic state (the stress for curve 2 is higher than that for curve 1).

Figure 15

Long-term shear-induced solid-to-liquid transition for 51% suspension of Kaolin.

Figure 16

Evolution of the storage G′ and loss G″ moduli in isothermal gelation at ω = const.

Figure 17

Amplitude dependences of the storage G′ (A) and loss G″ (A) components of the complex dynamic modulus showing the transition to the non-linear viscoelastic behavior at constant frequency.

Figure 18

Dependence of melting (T_m) and gelling (T_g) temperatures on the κ-carrageenan-to-gelatin mass ratio Z in mixed hydrogels; gelatin concentration C_G = 1.0 wt.%. Original data.

Figure 19

Experimental data illustrating an evolution of viscoelastic properties at the liquid-to-gel transition, according to a concept formulated in [176]. G′ (ω) and G″ (ω) are used in the reduced form, and the constants are omitted; every pair of curves corresponds to the different moments of the gelation.

Figure 20

Kinetics of gelation as followed by an increase of the dynamic modulus G* normalized by its limiting value, G*_t→∞, at C_G = 2 g/100 g and different concentrations of κ-carrageenan.

Figure 21

Typical evolution of viscosity over tine in the gelation process up to the gel point t*.