Inhomogeneous Canham-Helfrich Abscission in Catenoid Necks under Critical Membrane Mosaicity

Abstract

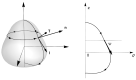
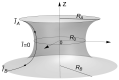
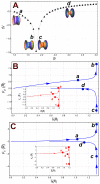
The mechanical effects of membrane compositional inhomogeneities are analyzed in a process analogous to neck formation in cellular membranes. We cast on the Canham-Helfrich model of fluid membranes with both the spontaneous curvature and the surface tension being non-homogeneous functions along the cell membrane. The inhomogeneous distribution of necking forces is determined by the equilibrium mechanical equations and the boundary conditions as considered in the axisymmetric setting compatible with the necking process. To establish the role played by mechanical inhomogeneity, we focus on the catenoid, a surface of zero mean curvature. Analytic solutions are shown to exist for the spontaneous curvature and the constrictive forces in terms of the border radii. Our theoretical analysis shows that the inhomogeneous distribution of spontaneous curvature in a mosaic-like neck constrictional forces potentially contributes to the membrane scission under minimized work in living cells.

Keywords: catenoidal necks; inhomogeneous spontaneous curvature; stress on curved fluid membranes.

Figure 1

Membrane neck dynamics under scissional forces. (A) A necking process describing the membrane necks connecting scissional compartments. Two modes of membrane necking are possible. (B) Symmetric mode: two spherical membranes compartments of equal radii joined by a catenoidal neck in a symmetric process. (C) Asymmetric mode: membrane compartment of different radii joined by an asymmetric catenoid.

Figure 2

A generic closed surface of revolution. In cylindrical coordinates $\{\rho ,\varphi ,z\}$, it is described with the embedding function: $\mathbf{X}(l,\varphi )=\rho \left(l\right)\mathit{\rho }+z\left(l\right)\mathbf{k}$ in the cylindrical basis $\mathit{\rho }=(cos\varphi ,sin\varphi ,0)$, $\mathbf{k}=(0,0,1)$ and $\mathit{\varphi }=(-sin\varphi ,cos\varphi ,0).$ The generating curve is parametrized with arc length l, so that ${{\rho }^{\prime }}^2+{z^{\prime }}^2=1$, while ${\rho }^{\prime }=cos\mathsf{\Psi }$ and $z^{\prime }=-sin\mathsf{\Psi }$, where $\mathsf{\Psi }$ is the tangential angle of the generating curve, and the derivative with respect to l is denoted as a ${}^{\prime }$. The unit normal can be written as $\mathbf{n}=sin\mathsf{\Psi }\mathit{\rho }+cos\mathsf{\Psi }\mathbf{k}$. The unit tangent vector, adapted to parallels on axially symmetric surfaces, is given by $\mathbf{T}=\mathit{\varphi },$ while the unit conormal is $\mathbf{l}=cos\mathsf{\Psi }\mathit{\rho }-sin\mathsf{\Psi }\mathbf{k}$. The orthonormal set $\{\mathbf{T},\mathbf{l},\mathbf{n}\}$ constitutes the Darboux basis adapted to the parallel loop.

Figure 3

Definition of the catenoid in terms of the equatorial radii $\left(R\right)$ and axial length $\left(L\right)$; $\overline{\rho }\equiv \rho /R_0$, $\overline{z}\equiv z/R_0$. The equation of the meridian catenary generator with fixed neck radii $R_0$ is given by $\overline{\rho }=cosh\overline{z}$. The catenoid can thus be re-parametrized in terms of the reduced arc length $\overline{l}\equiv l/R_0$, through the functions $\overline{\rho }=\sqrt{1+{\overline{l}}^2}$ and $\overline{z}=-\mathrm{arcsinh}\overline{l}$; in the upper border ${\overline{l}}_A=-\sqrt{{\overline{R}}_A^2-1}$, on the equatorial site, $\overline{l}=0$, and in the lower border ${\overline{l}}_B=\sqrt{{\overline{R}}_B^2-1}$. The relationship with the tangential angle of the generating curve: $sin\mathsf{\Psi }=1/\sqrt{1+{\overline{l}}^2}$, and $cos\mathsf{\Psi }=\overline{l}/\sqrt{1+{\overline{l}}^2}$. The derivative respect to $\overline{l}$ is given by ${\overline{\mathsf{\Psi }}}^{\prime }=-1/(1+{\overline{l}}^2)$. The area of each hemisphere is rescaled in terms of its corresponding border; thus, the rescaled surface area ${\overline{A}}_i\equiv A_i/\left(2\pi R_i^2\right)$ in the upper hemisphere, e.g., is given by $2{\overline{A}}_i\left({\overline{R}}_i\right)=\sqrt{{\overline{R}}_i^2-1}/{\overline{R}}_i+{\overline{R}}_i^{-2}\mathrm{arctanh}(\sqrt{{\overline{R}}_i^2-1}/{\overline{R}}_i^2)$, where ${\overline{R}}_i=\{{\overline{R}}_A,{\overline{R}}_B\}$. Similarly, the height is $\overline{h}={\overline{R}}_A^{-1}\mathrm{arcsinh}\left(\sqrt{{\overline{R}}_A^2-1}\right)+{\overline{R}}_B^{-1}\mathrm{arcsinh}\left(\sqrt{{\overline{R}}_B^2-1}\right)$.

Figure 4

Some stages along the transition of the symmetric catenoidal shape. In the upper panel, the stages (a–c), are in the subcritical regime $\overline{R}<{\overline{R}}^{†}\approx 1.81$, while the stages in the bottom panel (d–f), are in the supercritical regime $\overline{R}>{\overline{R}}^{†}$. The corresponding behavior of the spontaneous curvature, $\overline{K}\left(\overline{l}\right)$, and the local torque $\overline{m}\left(\overline{l}\right)$, is shown as a function of the arc length $\overline{l}$. Note the flip-flop behavior of these functions as passing the critical value ${\overline{R}}^{†}$.

Figure 5

(A): The energy of the radial interaction $\mathcal{U}\left(\overline{R}\right)$ (black triangles) between the boundaries of a symmetric catenoid (we have taken the experimental reference $\lambda =-1/0.7$). Some catenoidal points of reference along the path: $\mathbf{a}$ ($\overline{R}=1.2$), $\mathbf{b}$ ($\overline{R}=1.7$), $\mathbf{c}$ ($\overline{R}=1.9$), and $\mathbf{d}$ ($\overline{R}=3$). The first two points belong to the subcritical regime, and the last two points are in the supercritical sector. The critical point is at ${\overline{R}}^{*}\approx 1.81$. (B): The radial force $F_{\rho }$, on the lower border (right), as a function of $\overline{h}$ (the separation distance between the borders). The inset panel outline the radial force as a function of the area of the catenoid. (C): The axial force $F_z\equiv -\overline{\eta }$ as a function of $\overline{h}$ (the distance of separation between the borders). The inset panel shows the axial force as a function of the area $\overline{A}$.

Figure 6

Some stages along an asymmetric transition, such that the upper (left) radii is fixed to be ${\overline{R}}_A=2$. The critical point occurs at ${\overline{R}}^{*}\approx 1.65$, so that the first two stages (a,b), are in the subcritical regime while the last two (c,d), belong to the supercritical regime. Note that both functions, ${\overline{K}}_0\left(\overline{l}\right)$ and $\overline{m}\left(\overline{l}\right)$, are asymmetric functions along the corresponding catenoid.

Figure 7

Numerical results in the case of fixed radii ${\overline{R}}_A=1$ and $1/\lambda =-0.7$. (A): The energy of interaction $\mathcal{U}$ (black triangles) between the borders as a function of the radii ${\overline{R}}_B$. As reference, some catenoidal points have been identified along the way: $\mathbf{a}({\overline{R}}_B=1.5)$, $\mathbf{b}({\overline{R}}_B=5)$, and $\mathbf{c}({\overline{R}}_B=10)$. The distribution of the curvature ${\overline{K}}_0$ and the torque $\overline{m}$ have been depicted at the corresponding inset panel. (B): The radial force $F_{\rho }$, on the lower border as a function of $\overline{h}$, the distance of separation between the borders. The inset panel shown the radial force as a function of the area $\overline{A}$. The catenoid of maximal size reaches at ${\overline{R}}_B^{†}\approx 1.81$. Note that asymptotically, the area $\overline{A}\to 1/2$.