Study of Ultrasonic Guided Wave Propagation in Bone Composite Structures for Revealing Osteoporosis Diagnostic Indicators

Abstract

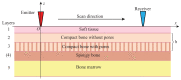
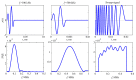
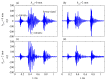
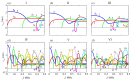
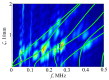
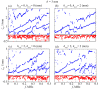
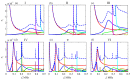
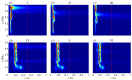
Tubular bones are layered waveguide structures composed of soft tissue, cortical and porous bone tissue, and bone marrow. Ultrasound diagnostics of such biocomposites are based on the guided wave excitation and registration by piezoelectric transducers applied to the waveguide surface. Meanwhile, the upper sublayers shield the diseased interior, creating difficulties in extracting information about its weakening from the surface signals. To overcome these difficulties, we exploit the advantages of the Green's matrix-based approach and adopt the methods and algorithms developed for the guided wave structural health monitoring of industrial composites. Based on the computer models implementing this approach and experimental measurements performed on bone phantoms, we analyze the feasibility of using different wave characteristics to detect hidden diagnostic signs of developing osteoporosis. It is shown that, despite the poor excitability of the most useful modes associated with the diseased inner layers, the use of the improved matrix pencil method combined with objective functions based on the Green's matrix allows for effective monitoring of changes in the elastic moduli of the deeper sublayers. We also note the sensitivity and monotonic dependence of the resonance response frequencies on the degradation of elastic properties, making them a promising indicator for osteoporosis diagnostics.

Keywords: composite bone phantoms; guided wave modal excitability; resonance diagnostics; restoration of effective elastic moduli.

Figure 1

(a) Phantom blanks: plexiglass plates drilled from below for different depths; (b) top view of plates drilled in a checkerboard pattern; (c) experimental setup; and (d) setup with a specimen covered by mammalian tissue.

Figure 2

Multilayer model of the bone composite structure and measurement scheme.

Figure 3

Examples of driving pulses $p\left(t\right)$ (top) and their frequency spectra $\left|P\right(f\left)\right|$ (bottom).

Figure 4

Examples of measured signals on the phantoms successively subjected to the three pulses shown in Figure 3: uncoated (a) and coated (b) samples with intact plates; and uncovered (c) and covered (d) 2/3 drilled plates; $h=3$ mm.

Figure 5

Examples of time–space waveform profiles measured at the 2/3 drilled phantoms ($h=$ 3 mm, $h_{pore}=$ 2 mm; left column) and intact thick-plate phantoms ($h=$ 6 mm, $h_{pore}=$ 0 mm; right column); uncoated (a,b) and coated with $h_{soft}=$ 2 mm (c,d) and $h_{soft}=$ 4 mm (e,f) soft layer; points’ spacing $\Delta x=1$ mm, time discrete $\Delta t=$ 0.03 μs. Straight lines emphasize the propagation of fast and slow wave packets.

Figure 6

Slowness dispersion curves for uncoated samples I–III (top, (a–c)) and coated phantoms IV–VI (bottom, (d–f)); $h=3$ mm.

Figure 7

Group velocities $v_n$ for the same samples as in Figure 6.

Figure 8

Scalogram images of the Green’s matrix element $|\omega K_{22}|$ in the frequency-slowness plane for the same phantoms I–III (top, (a–c)) and IV–VI (bottom, (d–f)) as in Figure 6 and Figure 7 above.

Figure 9

Depth dependencies of the $A_0$ and $S_0$ fundamental modes excited in uncoated plates I–III (blue and red lines in top subplots (a–c)), and of the first three modes in coated phantoms IV–VI (bottom, (d–f)), green lines are for the additional mode arising in the coated samples, horizontal black lines show interfaces between sublayers); $f=100$ kHz.

Figure 10

Lamb wave dispersion curves superimposed on the blurry spots of the H-function were calculated based on experimental data measured on the plexiglass plate of a thickness of 5 mm subjected to two pulses at $f_c=$ 100 and 300 kHz.

Figure 11

Wavenumbers ${\zeta }_n\left(f\right)$ extracted from experimental data by the double-sided MPM processing with $\delta =0.1$; blue and red points are for Re ${\zeta }_n$ and −Im ${\zeta }_n$, respectively.

Figure 12

The points from Figure 11 retained after H-filtering with $\epsilon =0.1$; blue and red points are for Re ${\zeta }_n$ and −Im ${\zeta }_n$, respectively.

Figure 13

Restoring the effective material parameters of the hard (plexiglass) layer (a) and its lower drilled part (b) from synthetic data calculated for phantoms I–VI; horizontal lines indicate that the input body wave velocities $c_p$ and $c_s$ and markers are for their restored values; sweep driving pulse, Figure 3, right.

Figure 14

Amplitudes of frequency spectra $a_n\left(f\right)$ of the guided waves generated in phantoms I–VI (solid lines) and their total sum (dashed lines); delta pulse, $P=1$.

Figure 15

Time--frequency wavelet images $|w_0(t,f)|$ of the synthetic signals $v_0\left(t\right)$ calculated for phantoms I–VI (sweep pulse); the vertical dashed lines indicate the beginning of tails in the calculations for Figure 16 and Figure 17 below.

Figure 16

Frequency spectra of the signals’ tails for phantoms I–VI; $h=3$ mm.

Figure 17

Diagrams of resonance frequencies $f_r$ depending on the sample structure for the peak patterns in Figure 16, uncovered (a) and covered (b) samples; the same for the h = 6 mm thick plate samples (c,d). Light blue and pink lines are for the resonance frequencies inherent in uncoated phantoms of thickness $h=3$ mm (a), which also appear and keep decreasing in coated samples (b); twice-thicker phantoms yield additional resonance (green line, (c)) that also keeps decreasing in covered samples (d).