Einstein Model of a Graph to Characterize Protein Folded/Unfolded States

Abstract

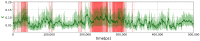
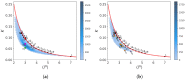
The folded structures of proteins can be accurately predicted by deep learning algorithms from their amino-acid sequences. By contrast, in spite of decades of research studies, the prediction of folding pathways and the unfolded and misfolded states of proteins, which are intimately related to diseases, remains challenging. A two-state (folded/unfolded) description of protein folding dynamics hides the complexity of the unfolded and misfolded microstates. Here, we focus on the development of simplified order parameters to decipher the complexity of disordered protein structures. First, we show that any connected, undirected, and simple graph can be associated with a linear chain of atoms in thermal equilibrium. This analogy provides an interpretation of the usual topological descriptors of a graph, namely the Kirchhoff index and Randić resistance, in terms of effective force constants of a linear chain. We derive an exact relation between the Kirchhoff index and the average shortest path length for a linear graph and define the free energies of a graph using an Einstein model. Second, we represent the three-dimensional protein structures by connected, undirected, and simple graphs. As a proof of concept, we compute the topological descriptors and the graph free energies for an all-atom molecular dynamics trajectory of folding/unfolding events of the proteins Trp-cage and HP-36 and for the ensemble of experimental NMR models of Trp-cage. The present work shows that the local, nonlocal, and global force constants and free energies of a graph are promising tools to quantify unfolded/disordered protein states and folding/unfolding dynamics. In particular, they allow the detection of transient misfolded rigid states.

Keywords: Kirchhoff index; Wiener index; graph theory; intrinsically disordered proteins; molecular dynamics; protein folding.

Figure 1

MD trajectory of Trp-cage at 380 K. Time t in red $(\forall t):\xi \left(t\right)>0.6$. The yellow curve is computed for a moving mean with a window size of 1 ns.

Figure 2

Evolution of the global force constant K for the MD trajectory shown in Figure 1. The bold green curve is computed for a moving mean with a window size of 1 ns.

Figure 3

Panels (a,b) represent respectively the PDF of ($\xi ,K$) values and ($\xi ,〈l^0〉$) computed from the trajectory shown in Figure 1.

Figure 4

Comparison between the average shortest path length (blue) and global force constant (green) for the MD trajectory shown in Figure 1. The bold green curve is computed for a moving mean with a window size of 1 ns. Times $t_0$, $t_1$, $t_2$, $t_3$, $t_4$, and $t_5$ discussed in the text are indicated.

Figure 5

Relationship between K and l computed for the MD trajectory in Figure 1. Panel (a) PDF of (K,$〈l^0〉$) (blue dots) and pairs of values (K,$〈l^0〉$) for three selected snapshots named $s_1$ (green dot), $s_2$ (pink dot), and $s_3$ (red dot) with the same value of $〈l^0〉$ as discussed in the text. Red line is the result of application of Equation (44). Black dots are the results of model chains with regular long distance spring force constants of different lengths named $(20,j=1,2,3\dots )$ in the main text. Panel (b) PDF of (K,$〈l^0〉$) from all snapshots with $\xi >0.6$ (blue). Red line and black dots are as in Panel (a). Orange dots are the (K,$〈l^0〉$) values of the experimental NMR models of Trp-cage (PDB ID: 12lY). Colors dots correspond to the values computed for the snapshots at times $t_0$ to $t_5$ indicated at Figure 4. Panels (c–k) are three-dimensional representations of the structures $s_1$, $s_2$, $s_3$ in Panel (a) and of the structures at times $t_0$, $t_1$, $t_2$, $t_3$, $t_4$, $t_5$, respectively. The spheres are the positions of the $C^{\alpha }$ atoms, and the tube represents the backbone. The black lines are the contacts considered to build the PG.

Figure 5

Relationship between K and l computed for the MD trajectory in Figure 1. Panel (a) PDF of (K,$〈l^0〉$) (blue dots) and pairs of values (K,$〈l^0〉$) for three selected snapshots named $s_1$ (green dot), $s_2$ (pink dot), and $s_3$ (red dot) with the same value of $〈l^0〉$ as discussed in the text. Red line is the result of application of Equation (44). Black dots are the results of model chains with regular long distance spring force constants of different lengths named $(20,j=1,2,3\dots )$ in the main text. Panel (b) PDF of (K,$〈l^0〉$) from all snapshots with $\xi >0.6$ (blue). Red line and black dots are as in Panel (a). Orange dots are the (K,$〈l^0〉$) values of the experimental NMR models of Trp-cage (PDB ID: 12lY). Colors dots correspond to the values computed for the snapshots at times $t_0$ to $t_5$ indicated at Figure 4. Panels (c–k) are three-dimensional representations of the structures $s_1$, $s_2$, $s_3$ in Panel (a) and of the structures at times $t_0$, $t_1$, $t_2$, $t_3$, $t_4$, $t_5$, respectively. The spheres are the positions of the $C^{\alpha }$ atoms, and the tube represents the backbone. The black lines are the contacts considered to build the PG.

Figure 6

Distribution of the local force constants at times $t_0$ (bold green), $t_1$ (light blue), $t_2$ (red), $t_3$ (brown), $t_4$ (dark blue) and $t_5$ (orange) indicated in Figure 4 and discussed in the text. The gray area limited by dashed lines represents the range of values observed in the MD trajectory.

Figure 7

Free-energy graph calculations for the trajectory of Figure 1. (a) Local (blue), nonlocal (green), global (red), and collective (black) free energy with $ϵ=0$. Horizontal dashed lines indicate the zero baselines of the free energies with the corresponding colors. (b) Enthalpy term of the free-energy graph with $ϵ=-1$ (blue), $ϵ=-3$ (green), and $ϵ=-5$ (dark red). Horizontal dashed line indicates the zero baseline. $d\left(t\right)\equiv {\sum }_i{d}_i\left(t\right)$ and $d\left(0\right)\equiv {\sum }_i{d}_i\left(0\right)$. (c) Local free energy with $ϵ=0$ (blue) and $ϵ=-5$ (green). Folded regions are indicated by red vertical lines as in Figure 1. Horizontal dashed lines indicate the zero baselines of the free energies with the corresponding colors.